Question

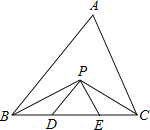
【题目】如图，已知在△ABC中，点D、E分别是AB、AC上一点，且AD=AE，∠ABE=∠ACD，BE与CD相交于点F．试判断△BCF的形状，并说明理由．

Answer 1

【答案】△BFC是等腰三角形．理由见解析

【解析】

试题分析：由于AD=AE，∠ABE=∠ACD，∠A为公共角，根据全等三角形的判定方法得到△ABE≌△ACD，则AB=AC，根据等腰三角形的性质有∠ABC=∠ACB，易得∠FBC=∠FCB，根据等腰三角形的判定即可得到△BFC是等腰三角形．

解：△BFC是等腰三角形．理由如下：

在△ABE和△ACD中，

，

∴△ABE≌△ACD．

∴AB=AC．

∴∠ABC=∠ACB．

∴∠ABC﹣∠ABE=∠ACB﹣∠ACD．

即∠FBC=∠FCB．

∴△BFC是等腰三角形．