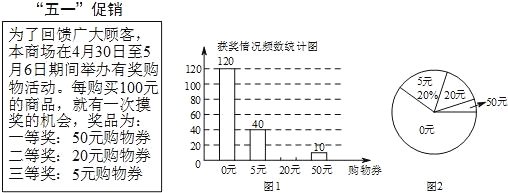
题目内容
【题目】如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
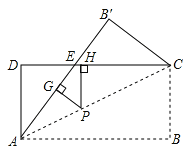
(1)试找出一个与△AED全等的三角形,并加以证明.
(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,试求PG+PH的值,并说明理由.
【答案】(1)△AED≌△CEB′;证明见解析;(2)4.
【解析】
试题分析:(1)由折叠的性质知,CB′=BC=AD,∠B=∠B′=∠D=90°,∠B′EC=DEA,则由AAS得到△AED≌△CEB′;
(2)延长HP交AB于M,则PM⊥AB,PG=PM,PG+PH=HM=AD,∵CE=AE=CD-DE=8-3=5在Rt△ADE中,由勾股定理得到AD=4,∴PG+PH=HM=AD=4.
试题解析:(1)△AED≌△CEB′
证明:∵四边形ABCD为矩形,
∴B′C=BC=AD,∠B′=∠B=∠D=90°,
又∵∠B′EC=∠DEA,
∴△AED≌△CEB′;
(2)由折叠的性质可知,∠EAC=∠CAB,
∵CD∥AB,
∴∠CAB=∠ECA,
∴∠EAC=∠ECA,
∴AE=EC=8-3=5.
在△ADE中,AD=![]() =4,
=4,
延长HP交AB于M,则PM⊥AB,
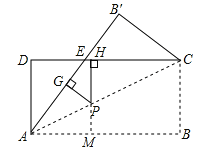
∴PG=PM.
∴PG+PH=PM+PH=HM=AD=4.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目