��Ŀ����
��֪�������εı߳�Ϊ1��1����ͼ�٣�������������εĶԽ���Ϊ
��
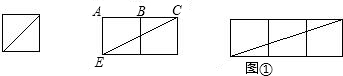
��2������ͼ�ڣ���֤��BCE�ס�BED��
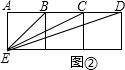
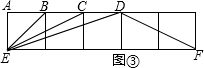
��3����ͼ�ۣ����������������������У�ͨ����������ѡ��һ����ȷ�Ľ��ۼ���֤����1����BEC+��BDE=45�㣻����BEC+��BED=45�㣻����BEC+��DFE=45��
ע�⣺����������Ծ�ȫ������Ľ����������ʱ����ͼ���з����µĽ��ۣ������Ӹ����ߺ�������ĸ��������֤�����������1��3�֣�
��������1����Ҫ�Ǹ��ݹ��ɶ���Ѱ�ҹ��ɣ��������������ҵ���ȷ���ۣ�
��2����ÿ���������У����ݹ��ɶ��������ÿ���ߵij��ȣ�����������߶�Ӧ�ɱ��������������������ж���
��3����֤��BEC+��DFE=45�㣬�ڱ����е���45��Ľ�������������AEB�͡�BEF��������֤������������ʱ��������������뷨ת�Ƶ���֪��һ������ȥ�����õ������ε�������⼴�ɣ�
��2����ÿ���������У����ݹ��ɶ��������ÿ���ߵij��ȣ�����������߶�Ӧ�ɱ��������������������ж���
��3����֤��BEC+��DFE=45�㣬�ڱ����е���45��Ľ�������������AEB�͡�BEF��������֤������������ʱ��������������뷨ת�Ƶ���֪��һ������ȥ�����õ������ε�������⼴�ɣ�
����⣺��1���ɹ��ɶ���֪���ڵ�һ��ͼ���У��Խ��߳�=
=
��
�ڶ���ͼ���У��Խ��߳�=
=
��
������ͼ���У��Խ��߳�=
=
��
���Ե�n��ͼ���У��Խ��߳�=
��
��2���ڡ�BCE�У�BC=1��BE=
��EC=
��
�ڡ�BED�У�BE=
��BD=2��ED=
��
����
=
=
=
��
���BCE�ס�BED��
��3��ѡȡ�ۣ�
��CD��EF����CE=DF��
���ı���CEFDΪ�������Σ�
���DFE=��CEF��
���BEC+��DFE=��BEC+��CEF=45�㣮
| 2 |
| 12+1 |
�ڶ���ͼ���У��Խ��߳�=
| 5 |
| 22+1 |
������ͼ���У��Խ��߳�=
| 10 |
| 32+1 |
���Ե�n��ͼ���У��Խ��߳�=
| n2+1 |
��2���ڡ�BCE�У�BC=1��BE=
| 2 |
| 5 |
�ڡ�BED�У�BE=
| 2 |
| 10 |
����
| BE |
| BC |
| BD |
| BE |
| ED |
| EC |
| 2 |
���BCE�ס�BED��
��3��ѡȡ�ۣ�
��CD��EF����CE=DF��
���ı���CEFDΪ�������Σ�
���DFE=��CEF��
���BEC+��DFE=��BEC+��CEF=45�㣮
������������Ҫ���������Ƶ��ж������ɶ��������á��������ε����ʣ�

��ϰ��ϵ�д�
 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д� �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
�����Ŀ
��֪һ�������εı߳�Ϊa�����ΪS��������
A��S=
| ||
| B��S��ƽ������a | ||
| C��a��S������ƽ���� | ||
D��a=��
|
