题目内容
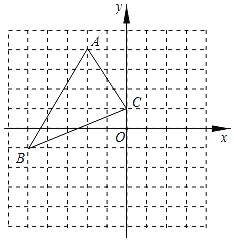
【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A![]() B
B![]() C
C![]() .
.
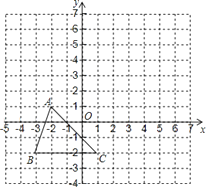
(1)在图中画出△A![]() B
B![]() C
C![]() ;
;
(2)写出点A![]() 、B
、B![]() 、C
、C![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
轴上是否存在一点P,使得△PBC与△ABC面积相等?若存在,写出点P的坐标;若不存在,说明理由.
【答案】(1)见解析;(2)A′(0,4),B′(-1,1),C′(3,1);(3)存在,点P的坐标是(0,1)或(0,-5).
【解析】
(1)分别把A,B,C三点向上平移3个单位长度,再向右平移2个单位长度即得A′,B′,C′三点连线即可;(2)可以先写出A,B,C三点坐标,然后分别把各点的横坐标加2,纵坐标加3即得A′,B′,C′坐标;(3)先把△ABC面积求出来,S△ABC=4×3÷2=6,若存在,设P点到BC的距离为x,BC=4,当△PBC与△ABC面积相等时,4x÷2=6,x=3,P点到BC的距离为3的点有2个为±3,当为3时,P点纵坐标是3-2=1,当为-3时,P点纵坐标是-3-2=-5,综上所述,y轴上存在点P,使得△PBC与△ABC面积相等,点P的坐标是(0,1)或(0,-5).
解:(1)分别把A,B,C三点向上平移3个单位长度,再向右平移2个单位长度即得A′,B′,C′,画出三角形A′B′C′;如图:
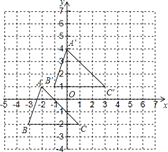
(2)由图写出A,B,C三点坐标:A(-2,1),B(-3,-2),C(1,-2),
∵上平移3个单位长度,右平移2个单位长度,
∴各点的横坐标加2,纵坐标加3得,:A′(0,4),B′(-1,1),C′(3,1).
(3)由图可知,S△ABC=4×3÷2=6,BC=4,设P点到BC的距离为x,4x÷2=6,x=3,
∵P点到BC的距离为3的点有2个为±3,
∴当为3时,P点纵坐标是3-2=1,当为-3时,P点纵坐标是-3-2=-5,P点横坐标是0,
∴点P的坐标是(0,1)或(0,-5).

 考前必练系列答案
考前必练系列答案