题目内容
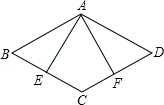
(2013年四川攀枝花6分)如图所示,已知在平行四边形ABCD中,BE=DF
求证:AE=CF.
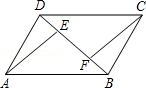
求证:AE=CF.

证明:∵BE=DF,∴BE﹣EF=DF﹣EF,即DE=BF。
∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC。∴∠ADE=∠CBF。
∵在△ADE和△CBF中, ,
,
∴△ADE≌△CBF(SAS),∴AE=CF。
∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC。∴∠ADE=∠CBF。
∵在△ADE和△CBF中,
 ,
,∴△ADE≌△CBF(SAS),∴AE=CF。
求出DE=BF,根据平行四边形性质求出AD=BC,AD∥BC,推出∠ADE=∠CBF,证出△ADE≌△CBF即可。

练习册系列答案
相关题目



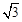 ,则AB的长是 .
,则AB的长是 .