题目内容
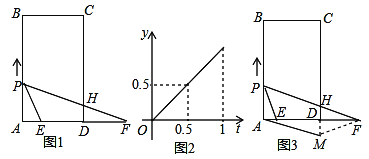
【题目】如图1,矩形ABCD中,AB=7cm,AD=4cm,点E为AD上一定点,F为AD延长线上一点,且DF=acm,点P从A点出发,沿AB边向点B以2cm/s的速度运动,运动到B点停止,连结PE,设点P运动的时间为ts,△PAE的面积为ycm2,当0≤t≤1时,△PAE的面积y(cm2)关于时间t(s)的函数图象如图2所示,连结PF,交CD于点H.
(1)t的取值范围为 ,AE cm;
(2)如图3,将△HDF沿线段DF进行翻折,与CD的延长线交于点M,连结AM,当a为何值时,四边形PAMH为菱形?
(3)在(2)的条件下求出点P的运动时间t.
【答案】(1)0≤t≤3.5,AE=1;
(2)a=4;
(3)P的运动时间为=![]() 秒.
秒.
【解析】证明:(1)∵AB=7,7÷2=3.5,
∴0≤t≤3.5,由题意可知y=![]() ×2t×AE,
×2t×AE,
∴由图象可知t=0.5时,y=0.5,
∴0.5=![]() ×2×0.5×AE,
×2×0.5×AE,
∴AE=1,
故答案分别为0≤t≤3.5,AE=1.
(2)如图3中,∵四边形AMHP是菱形,
∴AM=MH=2DM,AM∥PF,
∵∠ADM=90,∴∠MAD=30,
∴∠PFA=MFA=∠MAD=30,∴MA=MF,∵MD⊥AF,
∴AD=DF=4,∴a=4.
(3)∴当a=4cm时,此时FA=8cm,令PA=x,则PF=2x,根据勾股定理可得,PF2=PA2+AF2,
则(2x)2= x2+82,
解得x=![]() ,
,
∴P的运动时间为![]() ÷2=
÷2=![]() 秒.
秒.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目