题目内容
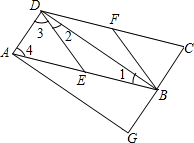
 已知:如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
已知:如图,在?ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
分析:(1)在证明全等时常根据已知条件,分析还缺什么条件,然后用(SAS,ASA,SSS)来证明全等;
(2)先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD是矩形.
(2)先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD是矩形.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=
AB,CF=
CD.
∴AE=CF.
在△AED与△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)解:当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形.
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=CF.
在△AED与△CBF中,
|

∴△ADE≌△CBF(SAS).
(2)解:当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形.
点评:本题主要考查了平行四边形的基本性质和矩形的判定及全等三角形的判定.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.三角形全等的判定条件:SSS,SAS,AAS,ASA.

练习册系列答案
相关题目
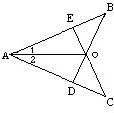 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,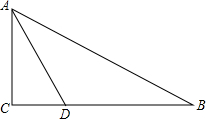 (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.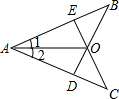 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,