��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬������OACB�Ķ���A��B�ֱ���x����y���ϣ���֪OA=3��OB=5����DΪy����һ�㣬������Ϊ��0��1������P�ӵ�A������ÿ��1����λ���ٶ����߶�AC��CB�ķ����˶�������P���B�غ�ʱֹͣ�˶����˶�ʱ��Ϊt�룮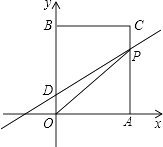
��1������P������Cʱ����ֱ��DP�ĺ�������ʽ��
��2�������OPD�����S����t�ĺ�������ʽ��
�ڵ���D����OP�ĶԳƵ�����x����ʱ�����P�����꣮
��3����P���˶��������Ƿ����ʹ��BDPΪ���������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺���ʱֱ��DP����ʽΪy=kx+b��
��D��0��1����C��3��5������ã� ![]() ��
��
��ã� ![]() ��
��
���ʱֱ��DP����ʽΪy= ![]() x+1
x+1
��2��
�⣺�ٵ���P���߶�AC��ʱ��OD=1����Ϊ3��S= ![]() ��
��
����P���߶�BC��ʱ��OD=1����Ϊ3+5��t=8��t��S= ![]() ��1����8��t��=��
��1����8��t��=�� ![]() t+4��
t+4��
�ڵ���D����OP�ĶԳƵ�����x����ʱ��D�ԳƵ�Ϊ��1��0������ʱֱ��OPΪy=x��
���ʱ��P�������ǣ�3��3��
��3��
�⣺���ڣ�����Ϊ��
����BDPΪ���������Σ�������������ǣ�
�ٵ�BD=BP1=OB��OD=5��1=4��
��Rt��BCP1��BD=4��BC=3��
���ݹ��ɶ����ã�CP1= ![]() =
= ![]() ��
��
��AP1=5�� ![]() ����P1��3��5��
����P1��3��5�� ![]() ����
����
�ڵ�BP2=DP2ʱ����ʱP2��3��3����
�۵�DB=DP3=4ʱ��
��Rt��DEP3��DE=3��
���ݹ��ɶ����ã�P3E= ![]() =
= ![]() ��
��
��AP3=AE+EP3= ![]() +1����P3��3��
+1����P3��3�� ![]() +1����
+1����
���ϣ����������P����Ϊ��3��3����3�� ![]() +1����3��5��
+1����3��5�� ![]() ����
����

����������1����ֱ��DP����ʽΪy=kx+b����D��B����������k��b��ֵ������ȷ��������ʽ����2���ٵ�P��AC��ʱ��������ODP��OD���Ϊ�̶�ֵ�������ʱ�������P��BC��ʱ���ױ�ODΪ�̶�ֵ����ʾ���ߣ������г�S��t�Ĺ�ϵʽ���ڵ�D����OP�ĶԳƵ�����x����ʱ��ֱ��OPΪy=x�������ʱP���꼴�ɣ���3�����ڣ��ֱ���BD��DP��BPΪ�ױ�����������ǣ����ù��ɶ�����ͼ���������������P���꼴�ɣ�
�����㾫����������Ҫ������һ�κ��������ʺ�һ�κ�����ͼ������ʵ����֪ʶ�㣬��Ҫ����һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С��һ�κ�����ֱ�ߣ�ͼ�������ޣ���������������,����ԭ��һֱ�ߣ�����ϵ��k��b,����֮��ĪС����k��б�ʶ��н�,b��Y�������,kΪ��������б,x����y������kΪ��������չ,�仯�������෴��k�ľ���ֵԽ��,��������ԽԶ������ȷ�����⣮

 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�����Ŀ��ij�̳�����һ�ֳɱ�Ϊ50Ԫ/����![]() �������������֣�������
�������������֣�������![]() �����������۵���
�����������۵���![]() ��Ԫ/��������һ�κ�����ϵ�������������±���
��Ԫ/��������һ�κ�����ϵ�������������±���
�ۼۣ�Ԫ/���� | ���� | 55 | 60 | 70 | ���� |
���������� | ���� | 75 | 70 | 60 | ���� |
��1����һ�κ���![]() �ı���ʽ��
�ı���ʽ��
��2�������̳��������ΪWԪ����д������W�����۵���![]() ֮��Ĺ�ϵʽ�����۵��۶�Ϊ����ʱ���̳��ɻ�����������������Ƕ��٣�
֮��Ĺ�ϵʽ�����۵��۶�Ϊ����ʱ���̳��ɻ�����������������Ƕ��٣�