Question

【题目】如图①所示，在正方形ABCD中，M是AB的中点，E是AB的延长线上一点，MN⊥DM，且交∠CBE的平分线于点N．

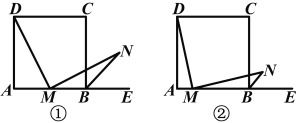
(1)求证：MD＝MN；

(2)若将上述条件中“M是AB的中点”改成“M是AB上任意一点”，其余条件不变，如图②所示，则结论“MD＝MN”还成立吗？若成立，给出证明；若不成立，请说明理由．

Answer 1

【答案】(1)证明：如图①所示，取AD的中点F，连接MF．

∵M是AB的中点，F是AD的中点，

∴，．

∵AB＝AD，∴AF＝AM＝DF＝MB，

∵∠1＝45°，∴∠DFM＝135°．

∵BN平分∠CBE，∴∠CBN＝45°．

∴∠MBN＝135°，∴∠MBN＝∠DFM．

∵MN⊥DM，∴△DMN＝90°，∴∠NMB＋∠DMA＝90°．

∵∠A＝90°，∴∠ADM＋∠DMA＝90°．

∴∠NMB＝∠ADM．

∴△DFM≌△MBN．∴MD＝MN．

(2)MD＝MN仍成立．

证明：如图②，在AD上取点F，使AF＝AM，连接MF．

由(1)中证法可得DF＝BM，∠DFM＝∠MBN，∠FDM＝∠BMN，

∴△DFM≌△MBN，∴MD＝MN．

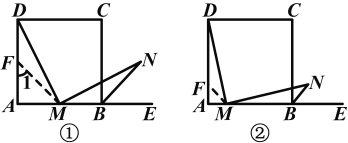
【解析】(1)证MD＝MN，可证它们所在的三角形全等，易知MN在钝角△MBN中，而MD在直角△AMD中，显然需添加辅助线构造全等三角形，由△MBN的特征想到可在AD上取AD的中点F，构造△MDF；(2)可参照第(1)题的方法论证．