题目内容
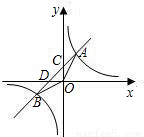
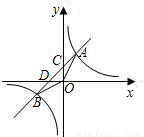
(2008•内江)如图,一次函数y=kx+b的图象经过第一、二、三象限,且与反比例函数图象相交于A,B两点,与y轴交于点C,与x轴交于点D,OB=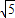 .且点B横坐标是点B纵坐标的2倍.
.且点B横坐标是点B纵坐标的2倍.(1)求反比例函数的解析式;
(2)设点A横坐标为m,△ABO面积为S,求S与m的函数关系式,并求出自变量的取值范围.
【答案】分析:(1)根据点B的横坐标是点B的纵坐标的2倍,且OB=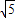 ,结合勾股定理,即可求出B点的坐标,从而求出反比例解析式;
,结合勾股定理,即可求出B点的坐标,从而求出反比例解析式;
(2)在(1)的基础上,当A点的横坐标已知的情况下,A点的纵坐标也可求出,把A、B的坐标代入一次函数解析式中,利用待定系数法,可求出解析式,从而可求出直线与坐标轴的交点.
再进一步利用求和的方法,求三角形ABO的面积时,可列出等量关系,从而得出函数解析式.
解答:解:(1)设点B的纵坐标为t,则点B的横坐标为2t.
根据题意,得(2t)2+t2=(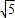 )2,
)2,
∵t<0,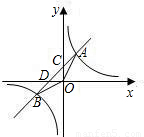
∴t=-1.
∴点B的坐标为(-2,-1).
设反比例函数为y=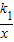 ,得
,得
k1=(-2)×(-1)=2,
∴反比例函数解析式为y=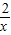 .
.
(2)设点A的坐标为(m,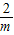 ).
).
根据直线AB为y=kx+b,可以把点A,B的坐标代入,
得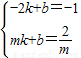 ,解得
,解得 .
.
∴直线AB为y=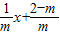 .
.
当y=0时, =0,
=0,
∴x=m-2,
∴点D坐标为(m-2,0).
∵S△ABO=S△AOD+S△BOD,
∴S= ×|m-2|×
×|m-2|×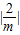 +
+ ×|m-2|×1,
×|m-2|×1,
∵m-2<0,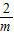 >0,
>0,
∴S=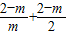 ,
,
∴S=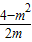 .
.
且自变量m的取值范围是0<m<2.
点评:此题考查了勾股定理、待定系数法以及数形结合思想,难易程度适中.
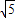 ,结合勾股定理,即可求出B点的坐标,从而求出反比例解析式;
,结合勾股定理,即可求出B点的坐标,从而求出反比例解析式;(2)在(1)的基础上,当A点的横坐标已知的情况下,A点的纵坐标也可求出,把A、B的坐标代入一次函数解析式中,利用待定系数法,可求出解析式,从而可求出直线与坐标轴的交点.
再进一步利用求和的方法,求三角形ABO的面积时,可列出等量关系,从而得出函数解析式.
解答:解:(1)设点B的纵坐标为t,则点B的横坐标为2t.
根据题意,得(2t)2+t2=(
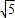 )2,
)2,∵t<0,

∴t=-1.
∴点B的坐标为(-2,-1).
设反比例函数为y=
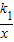 ,得
,得k1=(-2)×(-1)=2,
∴反比例函数解析式为y=
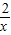 .
.(2)设点A的坐标为(m,
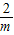 ).
).根据直线AB为y=kx+b,可以把点A,B的坐标代入,
得
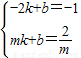 ,解得
,解得 .
.∴直线AB为y=
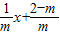 .
.当y=0时,
 =0,
=0,∴x=m-2,
∴点D坐标为(m-2,0).
∵S△ABO=S△AOD+S△BOD,
∴S=
 ×|m-2|×
×|m-2|×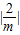 +
+ ×|m-2|×1,
×|m-2|×1,∵m-2<0,
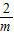 >0,
>0,∴S=
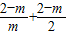 ,
,∴S=
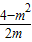 .
.且自变量m的取值范围是0<m<2.
点评:此题考查了勾股定理、待定系数法以及数形结合思想,难易程度适中.

练习册系列答案
相关题目
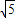 .且点B横坐标是点B纵坐标的2倍.
.且点B横坐标是点B纵坐标的2倍.