题目内容
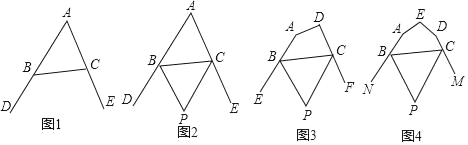
【题目】(1)如图1,在△ABC中,∠DBC与∠ECB分别为△ABC的两个外角,若∠A=60°,∠DBC+∠ECB多少度;
(2)如图2,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有怎样的数量关系?为什么?
(3)如图3,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A+∠D有怎样的数量关系?为什么?
(4)如图4,在五边形ABCDE中,BP、CP分别平分外角∠NBC、∠MCB,∠P与∠A+∠D+∠E有怎样的数量关系?(直接写出答案).
【答案】(1)∠DBC+∠ECB=240°;(2)∠P=90°﹣![]() ∠A;(3)∠P=180°﹣
∠A;(3)∠P=180°﹣![]() (∠A+∠D)(4)∠P=270°﹣
(∠A+∠D)(4)∠P=270°﹣![]() (∠A+∠E+∠D).
(∠A+∠E+∠D).
【解析】
(1)根据三角形内角和定理求出∠ABC+∠ACB,根据外角的性质计算;(2)根据角平分线的定义得到∠PBC=![]() ∠DBC,∠PCB=
∠DBC,∠PCB=![]() ∠ECB,根据三角形内角和定理计算;
∠ECB,根据三角形内角和定理计算;
(3)根据四边形内角和等于360°计算;(4)根据五边形的内角和等于540°、三角形的外角的性质、角平分线的定义计算.
(1)∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∴∠DBC+∠ECB=360°﹣120°=240°;
(2)∵BP、CP分别平分外角∠DBC、∠ECB,
∴∠PBC=![]() ∠DBC,∠PCB=
∠DBC,∠PCB=![]() ∠ECB,
∠ECB,
∴∠ABC+∠ACB=180°﹣∠A,
∴∠DBC+∠ECB=360°﹣(180°﹣∠A)=180°+∠A,
∴∠PBC+∠PCB=90°+![]() ∠A,
∠A,
∴∠P=180°﹣(∠PBC+∠PCB)=90°﹣![]() ∠A;
∠A;
(3)∴∠ABC+∠ACB=360°﹣∠A﹣∠D,
∴∠DBC+∠ECB=360°﹣(360°﹣∠A﹣∠D)=∠A+∠D,
∴∠PBC+∠PCB=![]() (∠A+∠D),
(∠A+∠D),
∴∠P=180°﹣![]() (∠A+∠D);
(∠A+∠D);
(4)五边形的内角和=(5﹣2)×180°=540°,
∴∠ABC+∠ACB=540°﹣∠A﹣∠E﹣∠D,
∴∠DBC+∠ECB=360°﹣(540°﹣∠A﹣∠E﹣∠D)=∠A+∠E+∠D﹣180°,
∴∠PBC+∠PCB=![]() (∠A+∠E+∠D﹣180°),
(∠A+∠E+∠D﹣180°),
∠P=180°﹣![]() (∠A+∠E+∠D﹣180°)=270°﹣
(∠A+∠E+∠D﹣180°)=270°﹣![]() (∠A+∠E+∠D).
(∠A+∠E+∠D).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案