题目内容
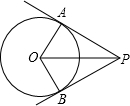
如图，PA、PB是⊙O的两条切线，切点是A、B．如果OP=4，PA=2
，那么∠AOB等于（ ）
| 3 |
| A．90° | B．100° | C．110° | D．120° |
∵△APO≌△BPO（HL），
∴∠AOP=∠BOP．
∵sin∠AOP=AP：OP=2
：4=
：2，
∴∠AOP=60°．
∴∠AOB=120°．
故选D．
∴∠AOP=∠BOP．
∵sin∠AOP=AP：OP=2
| 3 |
| 3 |
∴∠AOP=60°．
∴∠AOB=120°．
故选D．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
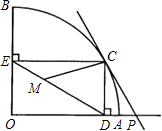点D，作CE⊥OB于点E，点M在DE上，DM=2EM，过点C的直线PC交OA的延长线于点P，且∠CPD=∠CDE．