题目内容
某商店将进价为每件80元的某种商品按每件100元出售,每天可售出100件.经过市场调查,发现这种商品每件每降低1元,其销售量就可增加10件.
(1)设每件商品降低售价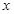 元,则降价后每件利润 元,每天可售出 件(用含
元,则降价后每件利润 元,每天可售出 件(用含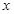 的代数式表示);
的代数式表示);
(2)如果商店为了每天获得利润2160元,那么每件商品应降价多少元?
(1)设每件商品降低售价
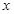 元,则降价后每件利润 元,每天可售出 件(用含
元,则降价后每件利润 元,每天可售出 件(用含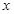 的代数式表示);
的代数式表示);(2)如果商店为了每天获得利润2160元,那么每件商品应降价多少元?
(1)(20-x),(100+10x);(2)2或8.
试题分析:(1)利润=售价-进价,降低1元增加10件,可知降低x元增加10x件,进而可用含x的代数式表示;
(2)将问题转化为求函数最值问题来解决,从而求出最大利润.
试题解析:(1)原来售价100,进价80,利润为20元,又降价x元后,利润为(20-x).
每降价一元,销量增加10件,说明降价x元,销量增加10x件,现在的销量为(100+10x);
(2)设每件商品降价x元.
(20-x)×(100+10x)=2160,
解得:x1=2,x2=8,
答:每件商品应降价2元或8元.
考点: 二次函数的应用.

练习册系列答案
相关题目
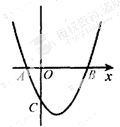
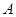 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与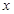 轴相交于点
轴相交于点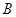 ,连结
,连结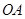 ,抛物线y=x
,抛物线y=x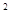
 从点
从点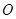 沿
沿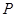 ,顶点
,顶点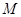 到
到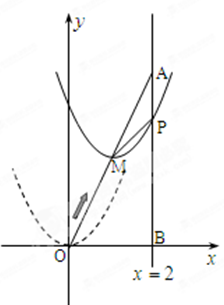
 ,
,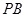 最短;
最短; ,使△
,使△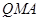 的面积与△
的面积与△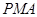 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点
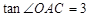 ,求抛物线的表达式;
,求抛物线的表达式;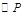 相离、相切、相交.
相离、相切、相交.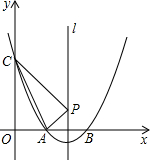



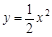 向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是
向左平移3个单位,再向下平移2个单位后,所得的抛物线的表达式是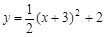
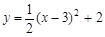

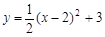
 的顶点坐标是( )
的顶点坐标是( )