题目内容
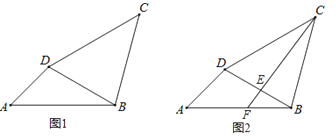
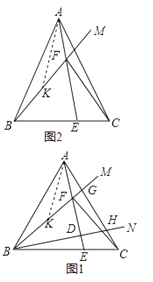
【题目】已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.
(1)如图1,若∠ABC=60°、∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.
①求证:CE=AG;
②若BF=2AF,连接CF,求∠CFE的度数;
(2)如图2,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,直接写出![]() 的结果
的结果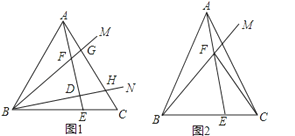
【答案】解:(1)①∵AB=AC,∠ABC=60°
∴△ABC为等边三角形,
则∠BAC=∠ACB=60°,AB=CA,
∵AD⊥BN,∠MBN=30°,
∴∠BFD=∠AFG=60°,
∵∠ABF+∠BAF=60°,
∠BAF+∠EAC=60°
∴∠EAC=∠GBA
在△GBA与△EAC中,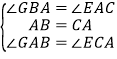 ,
,
∴△GBA≌△EAC,
∴CE=AG;
②如图1,取BF的中点K连接AK,
∵BF=2AF,
∴AF=BK=FK=![]() BF,
BF,
∴△FAK是等腰三角形,
∴∠FAK=∠FKA,
∵∠BFD=∠FAK+∠FKA=2∠AKF,
∵∠BFD=60°,
∴∠AKF=![]() ∠BFD=300
∠BFD=300
∵△GBA≌△EAC,
∴AG=CE,BG=AE,∠AGB=∠AEC,
∴KG=BG﹣BK=AE﹣AF=FE,
在△GAK与△EFC中,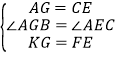 ,
,
∴△GAK≌△EFC,
∴∠CFE=∠AKF,
∴∠CFE=∠AKF=30°;
(2)如图2,在BF上取BK=AF,连接AK,
∵∠BFE=∠BAF+∠ABF,
∵∠BFE=∠BAC,
∴∠BAF+∠EAC=∠BAF+ABF,
∴∠EAC=∠FBA,
在△ABK与△ACF中, ,
,
∴△ABK≌△AFC,
∴S△ABK=S△ACF , ∠AKB=∠AFC,
∵∠BFE=2∠CFE,
∴∠BFE=2∠AKF,
∵∠BFE=2∠AKF=∠AKF+KAF,
∴∠AKF=∠KAF,
∴△FAK是等腰三角形,
∴AF=FK,
∴BK=AF=FK,
∴S△ABK=S△AFK ,
∵S△ABF=S△ABK+S△AFK=2S△ABK=2S△ACF ,
∴![]() =
=![]() .
.
故答案为:![]() .
.
【解析】(1)①由AB=AC,∠ABC=60°得到△ABC为等边三角形,根据等边三角形的性质得到∠BAC=∠ACB=60°,AB=CA,求得∠BFD=∠AFG=60°,推出∠EAC=∠GBA证得△GBA≌△EAC,根据全等三角形的性质即可得到结论;②如图1,取BF的中点K连接AK,由BF=2AF,推出△FAK是等腰三角形,根据等腰三角形的性质得到∠FAK=∠FKA,求得∠AKF=![]() ∠BFD=300 , 根据全等三角形的性质得到AG=CE,BG=AE,∠AGB=∠AEC,推出△GAK≌△EFC,根据全等三角形的性质得到∠CFE=∠AKF即可得到结论;
∠BFD=300 , 根据全等三角形的性质得到AG=CE,BG=AE,∠AGB=∠AEC,推出△GAK≌△EFC,根据全等三角形的性质得到∠CFE=∠AKF即可得到结论;
(2)如图2,在BF上取BK=AF,连接AK,推出∠EAC=∠FBA,根据全等三角形的性质得到S△ABK=S△ACF , ∠AKB=∠AFC,证得△FAK是等腰三角形,根据等腰三角形的性质得到AF=FK,即可得到结论.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案