题目内容
【题目】如图,等腰△BDC的顶点在等边三角形ABC的内部,∠BDC=90°,连接AD,过点D作一条直线将△ABD分割成两个等腰三角形,则分割出来的这两个等腰三角形的顶角度数分别是_____________.

【答案】120°和150°
【解析】如图,∵等腰△BDC的顶点在等边△ABC的内部,∠BDC=90°,
∴AB=AC,BD=CD,∠BAC=∠ABC=60°,∠DBC=45°,
∴∠ABD=60°-45°=15°.
∵在△ABD和ACD中: 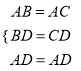 ,
,
∴△ABD≌△ACD,
∴∠BAD=∠CAD=![]() ∠BAC=30°,
∠BAC=30°,
∴过点D作直线把△ABD分割成两个等腰三角形,这两个等腰三角形的顶角度数分别为:(1)180°-30°-30°=120°;(2)180°-15°-15°=150°.
∴这两个等腰三角形的顶角的度数分别为120°和150°.


练习册系列答案
相关题目


