题目内容
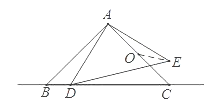
【题目】如图,正方形ABCD的边长为2,点E.F分别在边AD、CD上,∠EBF=45°,则△EDF
的周长等于_______。

【答案】4
【解析】∵四边形ABCD为正方形,
∴AB=BC,∠BAE=∠C=90,
∴把△ABE绕点A顺时针旋转90可得到△BCG,如图,
∴BG=AB,CG=AE,∠GBE=90,∠BAE=∠C=90,
∴点G在DC的延长线上,
∵∠EBF=45,
∴∠FBG=∠EBG∠EBF=45,
∴∠FBG=∠FBE,
在△FBG和△EBF中,
BF=BF,∠FBG=∠FBE,BG=BE,
∴△FBG≌△EBF(SAS),
∴FG=EF,
而FG=FC+CG=CF+AE,
∴EF=CF+AE,
∴△DEF的周长=DF+DE+CF+AE=CD+AD=2+2=4
故答案为:4.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目