题目内容
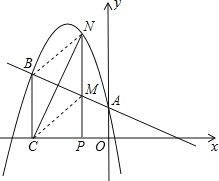
【题目】二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣![]() x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
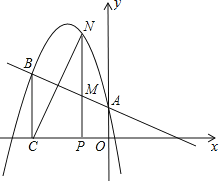
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
【答案】(1)y=﹣![]() ﹣
﹣![]() x+1;(2)
x+1;(2)![]() ;(3)当N(﹣1,4)时,BM和NC互相垂直平分.
;(3)当N(﹣1,4)时,BM和NC互相垂直平分.
【解析】
试题分析:方法一:
(1)首先求得A、B的坐标,然后利用待定系数法即可求得二次函数的解析式;
(2)设M的横坐标是x,则根据M和N所在函数的解析式,即可利用x表示出M、N的坐标,利用x表示出MN的长,利用二次函数的性质求解;
(3)BM与NC互相垂直平分,即四边形BCMN是菱形,则BC=MC,据此即可列方程,求得x的值,从而得到N的坐标.
方法二:
(1)略.
(2)求出点M,N的参数坐标,并得到MN的长度表达式,从而求出MN的最大值.
(3)因为BM与NC相互垂直平分,所以四边形BCMN为菱形,因为MN∥BC,所以只需MN=BC可得出四边形BCMN为平行四边形,再利用NC⊥BM进行求解.
方法一:
解:(1)由直线y=﹣![]() x+1可知A(0,1),B(﹣3,
x+1可知A(0,1),B(﹣3,![]() ),又点(﹣1,4)经过二次函数,
),又点(﹣1,4)经过二次函数,
根据题意得: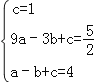 ,
,
解得: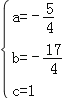 ,
,
则二次函数的解析式是:y=﹣![]() ﹣
﹣![]() x+1;
x+1;
(2)设N(x,﹣![]() x2﹣
x2﹣![]() x+1),
x+1),
则M(x,﹣![]() x+1),P(x,0).
x+1),P(x,0).
∴MN=PN﹣PM
=﹣![]() x2﹣
x2﹣![]() x+1﹣(﹣
x+1﹣(﹣![]() x+1)
x+1)
=﹣![]() x2﹣
x2﹣![]() x
x
=﹣![]() (x+
(x+![]() )2+
)2+![]() ,
,
则当x=﹣![]() 时,MN的最大值为
时,MN的最大值为![]() ;
;
(3)连接MC、BN、BM与NC互相垂直平分,
即四边形BCMN是菱形,
则MN=BC,且BC=MC,
即﹣![]() x2﹣
x2﹣![]() x=
x=![]() ,
,
且(﹣![]() x+1)2+(x+3)2=
x+1)2+(x+3)2=![]() ,
,
解x2+3x+2=0,得:x=﹣1或x=﹣2(舍去).
故当N(﹣1,4)时,BM和NC互相垂直平分.
方法二:
(1)略.
(2)设N(t,﹣![]() ),
),
∴M(t,﹣![]() t+1),
t+1),
∴MN=NY﹣MY=﹣![]() +
+![]() t﹣1,
t﹣1,
∴MN=﹣![]() ,
,
当t=﹣![]() 时,MN有最大值,MN=
时,MN有最大值,MN=![]() .
.
(3)若BM与NC相互垂直平分,则四边形BCMN为菱形.
∴NC⊥BM且MN=BC=![]() ,
,
即﹣![]() =
=![]() ,
,
∴t1=﹣1,t2=﹣2,
①t1=﹣1,N(﹣1,4),C(﹣3,0),
∴KNC=![]() =2,
=2,
∵KAB=﹣![]() ,
,
∴KNC×KAB=﹣1,
∴NC⊥BM.
②t2=﹣2,N(﹣2,![]() ),C(﹣3,0),
),C(﹣3,0),
∴KNC=![]() =
=![]() ,KAB=﹣
,KAB=﹣![]() ,
,
∴KNC×KAB≠﹣1,此时NC与BM不垂直.
∴满足题意的N点坐标只有一个,N(﹣1,4).

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案