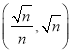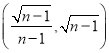题目内容
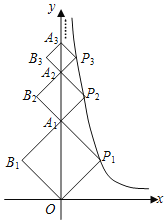
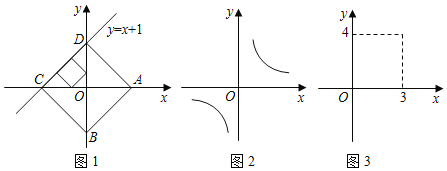
【题目】已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A.B.C.D各点依次排列)为正方形时,我们称这个正方形为此函数图象的“和谐正方形”.例如:在图1中,正方形ABCD是一次函数y=x+1图象的其中一个“和谐正方形”.
(1)如图1,若某函数是一次函数y=x+1,求它的图象的所有“和谐正方形”的边长;
(2)如图2,若某函数是反比例函数y=![]() (k>0),它的图象的“和谐正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;
(k>0),它的图象的“和谐正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;
(3)如图3,若某函数是二次函数y=ax2+c(a≠0),它的图象的“和谐正方形”为ABCD,C、D中的一个点坐标为(3,4),请求出该二次函数的解析式.
【答案】(1)![]() 或
或![]() ;(2)1,y=
;(2)1,y=![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)利用正方形的性质确定相关点的坐标从而计算正方形的边长,注意有两种情况.
(2)因为ABCD为正方形,所以可作垂线得到等腰直角三角形,利用点D(2,m)的坐标表示出点C的坐标从而求解.
(3)由题意得抛物线开口既可能向上,也可能向下.当抛物线开口向上时,正方形的另一个顶点也是在抛物线上,这个点既可能在点(3,4)的左边,也可能在点(3,4)的右边,过点(3,4)向x轴作垂线,利用全等三角形确定线段的长即可确定抛物线上另一个点的坐标;当抛物线开口向下时也是一样地分为两种情况来讨论.
解:(1)(I)当点A在x轴正半轴、点B在y轴负半轴上时:
∵四边形ABCD是正方形,一次函数y=x+1的图象与坐标轴的交点为C,D,
∴D(0,.1),C(﹣1,0),
∴OD=OD=1,
∴![]() =
=![]() =
=![]() ,
,
∴正方形ABCD的边长为![]() .
.
(II)当点A在x轴负半轴、点B在y轴正半轴上时:
设正方形边长为a,易得3a=![]() ,
,
解得a=![]() ,此时正方形的边长为
,此时正方形的边长为![]() .
.
∴所求“和谐正方形”的边长为![]() 或
或![]() ;
;
(2)如图,作DE⊥x轴,CF⊥y轴,垂足分别为点E、F,
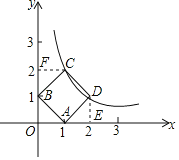
∵四边形ABCD是正方形,
∴∠CBA=∠DAB=90°,BC=BA=AD,
∵∠CFB=∠BOA=∠DEA=90°
∴∠FBC=∠BAO=∠ADE,
∴△ADE≌△BAO≌△CBF(AAS).
∵点D的坐标为(2,m),m<2,
∴DE=OA=BF=m,
∴OB=AE=CF=2﹣m.
∴OF=BF+OB=2,
∴点C的坐标为(2﹣m,2).
∴2m=2(2﹣m),解得m=1.
∴反比例函数的解析式为y=![]() ;
;
(3)实际情况是抛物线开口向上的两种情况中,另一个点都在(3,4)的左侧,而开口向下时,另一点都在(3,4)的右侧,与上述解析明显不符合,
①当点A在x轴正半轴上,点B在y轴正半轴上,点C坐标为(3,4)时:另外一个顶点为(4,1),对应的函数解析式是y=![]() ;
;
②当点A在x 轴正半轴上,点 B在 y轴正半轴上,点D 坐标为(3,4)时:不存在,
③当点A 在 x 轴正半轴上,点 B在 y轴负半轴上,点C 坐标为(3,4)时:不存在;
④当点A在x 轴正半轴上,点B在y轴负半轴上,点D坐标为(3,4)时:另外一个顶点C为(﹣1,3),对应的函数的解析式是y=![]() ;
;
⑤当点A在x轴负半轴上,点B在y轴负半轴上,点C坐标为(3,4)时,另一个顶点D的坐标是(7,﹣3)时,对应的函数解析式是y=![]() ;
;
⑥当点A在x轴负半轴上,点B在y轴负半轴上,点C坐标为(3,4)时,另一个顶点D的坐标是(﹣4,7)时,对应的抛物线为y=![]() ;
;
综合以上可得二次函数的解析式分别为:![]() 或
或![]() 或
或![]() 或
或![]()

 阅读快车系列答案
阅读快车系列答案【题目】某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查,分别随机抽取了50件产品并对某一项关键质量指标做检测,获得了它们的质量指标值s,并对样本数据(质量指标值s)进行了整理、描述和分析.下面给出了部分信息.
a.该质量指标值对应的产品等级如下:
质量指标值 |
|
|
|
|
|
等级 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
说明:等级是一等品,二等品为质量合格(其中等级是一等品为质量优秀).
等级是次品为质量不合格.
b.甲企业样本数据的频数分布统计表如下(不完整).
c.乙企业样本数据的频数分布直方图如下.
甲企业样本数据的频数分布表
分组 | 频数 | 频率 |
| 2 | 0.04 |
| m | |
| 32 | n |
| 0.12 | |
| 0 | 0.00 |
合计 | 50 | 1.00 |
乙企业样本数据的频数分布直方图
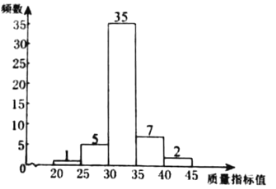
d.两企业样本数据的平均数、中位数、众数、极差、方差如下:
平均数 | 中位数 | 众数 | 极差 | 方差 | |
甲企业 | 31.92 | 32.5 | 34 | 15 | 11.87 |
乙企业 | 31.92 | 31.5 | 31 | 20 | 15.34 |
根据以上信息,回答下列问题:
(1)m的值为________,n的值为________.
(2)若从甲企业生产的产品中任取一件,估计该产品质量合格的概率为________;若乙企业生产的某批产品共5万件,估计质量优秀的有________万件;
(3)根据图表数据,你认为________企业生产的产品质量较好,理由为______________.(从某个角度说明推断的合理性)
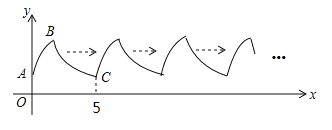
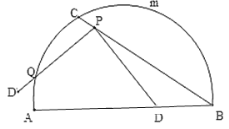
【题目】如图,C是![]() 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转![]() 得到线段
得到线段![]() .射线
.射线![]() 与
与![]() 交于点Q.已知
交于点Q.已知![]() ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离![]() ,P,Q两点的距离为
,P,Q两点的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() ,与x的几组对应值:
,与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.50 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
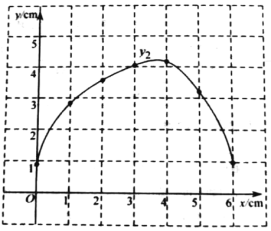
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)