题目内容
如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P、Q分别从A、C同时出发,点P以每秒3cm的速度向B移动,一直达到B止,点Q以每秒2cm的速度向D移动.

(1)P、Q两点出发后多少秒时,四边形PBCQ的面积为36cm2;
(2)是否存在某一时刻,使PBCQ为正方形?

(1)P、Q两点出发后多少秒时,四边形PBCQ的面积为36cm2;
(2)是否存在某一时刻,使PBCQ为正方形?
(1)4秒时;(2)不存在。
试题分析:(1)首先设P、Q两点出发后x秒时,四边形PBCQ的面积为36cm2,根据题意可得PB=AB-AP=(16-3x)cm,CQ=2xcm,再根据梯形的面积公式可得方程[(16-3x)+2x]×6×
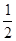 =36,再解方程即可;
=36,再解方程即可;(2)首先设P、Q两点出发后x秒时,四边形PBCQ是正方形,根据正方形的性质可得BP=BC,由此可得方程16-3x=6,解出x的值,再把x计算CQ的长度,发现CQ≠BC,故不存在使PBCQ为正方形的时刻.
(1)设P、Q两点出发后x秒时,四边形PBCQ的面积为36cm2,由题意得:
[(16-3x)+2x]×6×
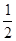 =36,解得:x=4.
=36,解得:x=4.答:P、Q两点出发后4秒时,四边形PBCQ的面积为36cm2.
(2)不存在,
理由:设P、Q两点出发后x秒时,四边形PBCQ是正方形,由题意得:
16-3x=6,解得
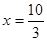 ,
,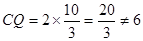 ,
,∴没有一个时刻可以使四边形PBCQ是正方形.
点评:解答本题的关键是熟练掌握正方形的性质,根据题意灵活选用恰当的性质。

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
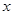 的方程
的方程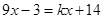 有整数解,那么满足条件的所有整数
有整数解,那么满足条件的所有整数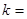 。
。 是关于
是关于 的一元一次方程,则
的一元一次方程,则 =
=