题目内容
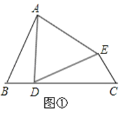
【题目】如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点E.
求证:(1)DE⊥AE;
(2)AE+CE=AB.

【答案】证明见解析
【解析】
(1)连接OD,根据等腰三角形的性质结合角平分线的性质可得出∠CAD=∠ODA,利用“内错角相等,两直线平行”可得出AE∥OD,结合切线的性质即可证出DE⊥AE;
(2)过点D作DM⊥AB于点M,连接CD、DB,根据角平分线的性质可得出DE=DM,结合AD=AD、∠AED=∠AMD=90°即可证出△DAE≌△DAM(SAS),根据全等三角形的性质可得出AE=AM,由∠EAD=∠MAD可得出![]() ,进而可得出CD=BD,结合DE=DM可证出Rt△DEC≌Rt△DMB(HL),根据全等三角形的性质可得出CE=BM,结合AB=AM+BM即可证出AE+CE=AB.
,进而可得出CD=BD,结合DE=DM可证出Rt△DEC≌Rt△DMB(HL),根据全等三角形的性质可得出CE=BM,结合AB=AM+BM即可证出AE+CE=AB.
(1)连接OD,如图1所示.
∵OA=OD,AD平分∠BAC,
∴∠OAD=∠ODA,∠CAD=∠OAD,
∴∠CAD=∠ODA,
∴AE∥OD.
∵DE是⊙O的切线,
∴∠ODE=90°,
∴OD⊥DE,
∴DE⊥AE.
(2)过点D作DM⊥AB于点M,连接CD、DB,如图2所示.
∵AD平分∠BAC,DE⊥AE,DM⊥AB,
∴DE=DM.
在△DAE和△DAM中,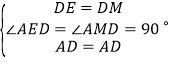 ,
,
∴△DAE≌△DAM(SAS),
∴AE=AM.
∵∠EAD=∠MAD,
∴![]() ,
,
∴CD=BD.
在Rt△DEC和Rt△DMB中,![]() ,
,
∴Rt△DEC≌Rt△DMB(HL),
∴CE=BM,
∴AE+CE=AM+BM=AB.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目