题目内容
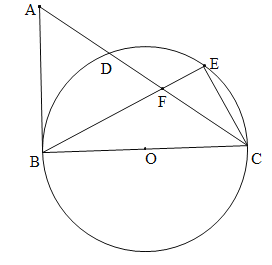
【题目】如图,在△ABC中,∠ABC=90°,以BC为直径作⊙O,交AC于D.E为![]() 的中点,连接CE,BE,BE交AC于F.
的中点,连接CE,BE,BE交AC于F.
(1)求证:AB=AF;
(2)若AB=3,BC=4,求CE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)先证明∠EBC=∠ECF, 再证明∠ABF=∠AFB,即可得AB=AF;
(2)先应用勾股定理求出AC的长,用AC-AF求出CF的长,再应用△EFC∽△ECB可求出CE的长.
试题解析:解:(1)证明:∵BC直径为⊙O的直径,∴∠BEC=90°,∴∠ECF+∠EFC=90°.
∵∠ABC=90°,∴∠ABF+∠EBC=90°.又∵E为![]() 的中点,∴∠EBC=∠ECF,∴∠EFC=∠ABF.又∵∠AFB=∠EFC,∴∠AFB=∠ABF,∴AB=AF;
的中点,∴∠EBC=∠ECF,∴∠EFC=∠ABF.又∵∠AFB=∠EFC,∴∠AFB=∠ABF,∴AB=AF;
(2)∵∠ABC=90°,∴AC=![]() =
=![]() =5.又∵AB=AF=3,∴CF=AC-AF=5-3=2.∵∠EBC=∠ECF,∠E=∠E,∴△EFC∽△ECB.∴
=5.又∵AB=AF=3,∴CF=AC-AF=5-3=2.∵∠EBC=∠ECF,∠E=∠E,∴△EFC∽△ECB.∴![]() .∴BE=2CE.∵∠BEC=90°,∴
.∴BE=2CE.∵∠BEC=90°,∴![]() ,∴
,∴![]() ,∴CE=
,∴CE=![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目