题目内容
【题目】抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)设![]() ,求该抛物线的解析式;
,求该抛物线的解析式;
(2)在⑴中,若点![]() 为直线
为直线![]() 下方抛物线上一动点,当⊿
下方抛物线上一动点,当⊿![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)是否存在整数![]() 使得
使得![]() 和
和![]() 同时成立,请证明你的结论.
同时成立,请证明你的结论.
【答案】(1)抛物线解析式为![]() ;
;
(2)![]() ;
;
(3)不存在整数![]() 使得
使得![]() 和
和![]() 同时成立,证明见解析.
同时成立,证明见解析.
【解析】试题分析:本题的⑴问中由于抛物线上没有现成的坐标,所以要根据一元二次方程根与系数的关系,并结合三角函数和二次函数的对称轴进行多次代数转换即可求出二次函数的待定系数![]() ,其转换有点繁琐,可以分步进行.
,其转换有点繁琐,可以分步进行.
关于面积的“最值”问题一般都要通过建立二次函数切入来解决问题,本题的⑵问可采用“割补法”来表示⊿![]() 的面积.若采取“补”的办法,可以连接
的面积.若采取“补”的办法,可以连接![]() ,此时⊿
,此时⊿![]() 的面积可以看作是四边形
的面积可以看作是四边形![]() 的面积减去⊿
的面积减去⊿![]() 的面积,即
的面积,即![]() ⊿
⊿![]() =
= ![]() ⊿
⊿![]() + (或 -)
+ (或 -)![]() ⊿
⊿![]() -
- ![]() ⊿
⊿![]() ,由于在⑴问中我们能把原二次函数的解析式求出来,在此基础上求出
,由于在⑴问中我们能把原二次函数的解析式求出来,在此基础上求出![]() 的坐标,然后把
的坐标,然后把![]() 的横纵坐标均用自变量表示出来,在此基础上建立关于⊿
的横纵坐标均用自变量表示出来,在此基础上建立关于⊿![]() 的面积的二次函数使问题可以解决.(本问也可以采用过点
的面积的二次函数使问题可以解决.(本问也可以采用过点![]() 作
作![]() 轴的垂线把⊿
轴的垂线把⊿![]() “割”成两个三角形来解答,计算量相当.)
“割”成两个三角形来解答,计算量相当.)
本题的⑶问是一个存在性的问题.先假设存在,然后结合![]() 和
和![]() 利用根与系数的关系解出
利用根与系数的关系解出![]() 的分别的整数值,在此基础上分析图象信息所得出的条件,分别代入讨论,即可使问题获得解决.
的分别的整数值,在此基础上分析图象信息所得出的条件,分别代入讨论,即可使问题获得解决.
试题解析:(1)根据题中的![]()
可知: 
∴![]() ,
,
配方得: ![]() .分别代入得:
.分别代入得: ![]() ①
①
∵![]()
∴![]() ;
;
又抛物线与![]() 轴的交点为
轴的交点为![]() ,
,
∴![]()
∵抛物线对称轴为![]() ,
,
即![]() ,
,
又![]() ,
,
∴![]() .
.
∴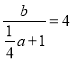 ②,
②,
把①②联立后解得: ![]() 或
或![]() (舍去).
(舍去).
把![]() 代入①得:
代入①得: ![]() .
.
∴抛物线解析式为![]() .
.
⑵.连结![]() ,过点
,过点![]() 分别向坐标作高
分别向坐标作高![]() (见后面的图示)
(见后面的图示)

若设点![]() 的横坐标为
的横坐标为![]() ,代入
,代入![]() 后得到
后得到![]() ,
,
即点![]() 的横纵坐标为
的横纵坐标为![]() .
.
则![]() .
.
在![]() 中,令
中,令![]() 时,
时, ![]() ;
;
即与![]() 轴交于点
轴交于点![]() 的坐标为
的坐标为![]() .
.
令![]() 时,解得:
时,解得: ![]()
即与![]() 轴交于点
轴交于点![]() 的坐标为
的坐标为![]() .
.
∴![]() ⊿
⊿![]() =
= ![]() ⊿
⊿![]() +
+ ![]() ⊿
⊿![]() -
- ![]() ⊿
⊿![]() =
= ![]()
①当![]() 时,
时, ![]() .
.
∵二次项系数![]()
∴![]() 没有最大值.
没有最大值.
②当![]() 时,
时, ![]() .
.
∵二次项系数![]()
∴![]() 有最大值.当
有最大值.当![]() 时,
时, ![]() 有最大值
有最大值![]() .
.
∴![]() .
.
⑶假设存在整数![]() ,并且使得
,并且使得![]() 和
和![]() 同时成立.、
同时成立.、
根据题意有: ![]() 即
即
解得: ![]()
∵![]() 为整数
为整数
∴![]()
对于抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点.
两点.
若要同时存在![]() 和
和![]() 说明:
说明:
①此时的抛物线开口向上且与![]() 轴在
轴在![]() 两个点之间(不含这两个点)有两个交点.;
两个点之间(不含这两个点)有两个交点.;
②当![]() 时,
时, ![]() ;
;
③当![]() 时,
时, ![]() .
.
∴ ①![]() ;②
;②![]() ;③
;③![]() ; 又④
; 又④![]() 要为整数.
要为整数.
∴把![]() 代入①②③④解得
代入①②③④解得![]() 无解;
无解;
把![]() 代入①②③④解得
代入①②③④解得![]() 无解;
无解;
把![]() 代入①②③④解得
代入①②③④解得![]() 无解.
无解.
综上所述不存在整数![]() 使得
使得![]() 和
和![]() 同时成立.
同时成立.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案