题目内容
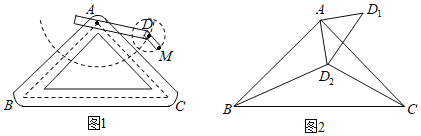
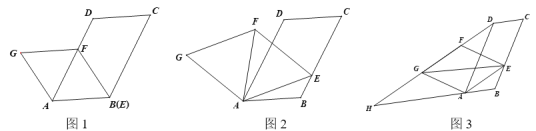
【题目】在图1,2,3中,已知□ABCD,∠ABC=120°,点E为线段BC上的动点,连接AE,以AE为边向上作菱形AEFG,且∠EAG=120°.
(1)如图1,当点E与点B重合时,∠CEF=______°;
(2)如图2,连接AF.
①填空:∠FAD_______∠EAB(填“>”,“=”,“<”);
②求证:点F在∠ABC的平分线上;
(3)如图3,连接EG,DG,并延长DG交BA的延长线于点H,当四边形AEGH是平行四边形时,求![]() 的值.
的值.
【答案】(1)60;(2)①=,②见解析;(3)3
【解析】
(1)根据菱形的性质计算即可;
(2)①证明∠DAB=∠FAE=60°,根据角的运算解答;
②作FM⊥BC于M,FN⊥BA交BA的延长线于N,证明△FAN≌△FME,根据全等三角形的性质得到FN=FM,根据角平分线的判定定理证明结论;
(3)根据直角三角形的性质得到GH=2AH,证明四边形ABEH为菱形,根据菱形的性质计算,得到答案.
解:(1)当E与点B重合时,∠EAG=120°,∵四边形GABF为菱形,
∴∠ABF=60°,∠CEF=120°-60°=60°
故答案为60°
(2)① =
∵四边形GABF为菱形;∴AF平分∠GAE,∠FAE=120°÷2=60°
∠DAB=60°,∠FAD=60°-∠DAE;∠EAB=60°-∠DAE
∴∠FAD=∠EAB
②证明:过F点做AB和BC的垂线垂足分别为M,N
由①可得三角形AEF为等边三角形
∠FAN=180°-60°-∠EAB=120°-∠EAB
∠FEM=60°+∠AEB=60°+(180°-120°-∠EAB)=120°-∠EAB
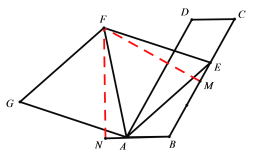
∴∠FAN=∠FEM
在FNA和FME中
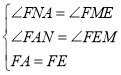
∴△FNA≌△FME(AAS)
∴FN=FM,
∴F在∠ABC的角平分线上
(3)当四边形AEGH为平行四边形时,可得GE//BH;
由四边形AEFG为菱形,可得GE平分∠FEA,∠GEA=30°
∴∠EAB=30°,AEB为等腰三角形;不妨设AB=x;可得AE=![]()
∵AE=GH;AGH为等腰三角形∴AH=![]() =3x
=3x
∠DAB=60°,∠H=30°,∴HAD为等腰三角形,可得AD=3x
BC=AD=3x
∴![]()