题目内容
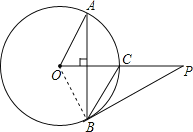
【题目】已知P是⊙O外一点,PO交⊙O于点C,OC=CP=2,弦AB⊥OC,∠AOC的度数为60°,连接PB.
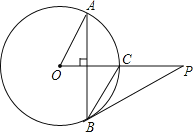
(1)求BC的长;
(2)求证:PB是⊙O的切线.
【答案】(1)BC=2;(2)见解析
【解析】
试题分析:(1)连接OB,根据已知条件判定△OBC的等边三角形,则BC=OC=2;
(2)欲证明PB是⊙O的切线,只需证得OB⊥PB即可.
(1)解:如图,连接OB.
∵AB⊥OC,∠AOC=60°,
∴∠OAB=30°,
∵OB=OA,
∴∠OBA=∠OAB=30°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC的等边三角形,
∴BC=OC.
又OC=2,
∴BC=2;
(2)证明:由(1)知,△OBC的等边三角形,则∠COB=60°,BC=OC.
∵OC=CP,
∴BC=PC,
∴∠P=∠CBP.
又∵∠OCB=60°,∠OCB=2∠P,
∴∠P=30°,
∴∠OBP=90°,即OB⊥PB.
又∵OB是半径,
∴PB是⊙O的切线.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目