题目内容
【题目】如图,已知AB∥DE,∠ABC=80°,∠CDE=140°,则∠C=( ) 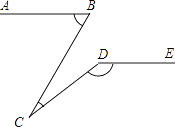
A.20°
B.30°
C.40°
D.50°
【答案】C
【解析】解:延长ED交BC于F, ∵AB∥DE,∴∠3=∠ABC=80°,∠1=180°﹣∠3=180°﹣80°=100°,
∠2=180°﹣∠CDE=180°﹣140°=40°,
在△CDF中,∠1=100°,∠2=40°,
故∠C=180°﹣∠1﹣∠2=180°﹣100°﹣40°=40°.
故选C.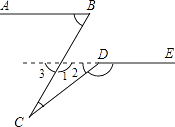
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补),还要掌握三角形的内角和外角(三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角)的相关知识才是答题的关键.

练习册系列答案
相关题目