题目内容
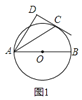
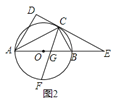
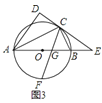
【题目】小明将三角形纸片ABC(AB >AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图②).小明认为△AEF是等腰三角形,你同意吗?如果同意,请你给出证明,如果不同意,请说明理由.

【答案】见解析
【解析】
由三角形纸片ABC(AB >AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,可得∠BAD=∠CAD,再次折叠该三角形纸片,使点A和点D重合,折痕为EF,可得EF垂直平分AD ,得AO="DO," ∠AOE=∠AOF=90°,所以△AEO≌△AFO,所以△AEF是等腰三角形.
解:同意
理由:如图,设AD与EF交于点G.由第一次折叠得∠BAD=∠CAD 
由第二次折叠得EF⊥AD
∴∠AGE=∠DGE=90°,
∴∠AGE=∠AGF=90°,
∴∠AEF=∠AFE.
∴AE=AF,
即△AEF为等腰三角形.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目