Question

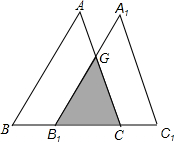如图，将△ABC沿BC方向平移得到△A₁B₁C₁，已知BC=

2

cm，△ABC与△A₁B₁C₁重叠部分（图中阴影部分）的面积是△ABC面积的一半，则△ABC平移的距离是

（

2

-1）

cm．

Answer 1

分析：根据平移的性质判定△ABC与△B₁CG相似，然后根据相似三角形面积的比等于相似比的平方求出B₁C的长度，再根据BB₁=BC-B₁C，计算即可得解．

解答：解：如图，根据平移的性质，AB∥A₁B₁，
∴△GB₁C∽△ABC，
∵重叠部分（图中阴影部分）的面积是△ABC的一半，
∴（

B1C

BC

）²=

1

2

，
∵BC=

2

cm，
∴B₁C=1cm，
∴₁=（

2

-1）cm，
故答案为：（

2

-1）．

点评：本题考查了平移的性质，相似三角形的判定与性质，判定出两三角形相似，利用相似三角形面积的比等于相似比的平方求出B₁C的长度是解题的关键．