题目内容
【题目】甲、乙两工程队同时修筑水渠,且两队所修水渠总长度相等.如图是两队所修水渠长度y(米)与修筑时间x(时)的函数图象的一部分.请根据图中信息,解答下列问题: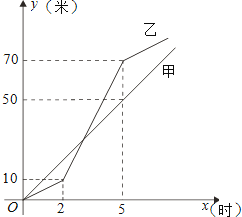
(1)①直接写出甲队在0≤x≤5的时间段内,y与x之间的函数关系式;
②直接写出乙队在2≤x≤5的时间段内,y与x之间的函数关系式;
(2)求开修几小时后,乙队修筑的水渠长度开始超过甲队?
(3)如果甲队施工速度不变,乙队在修筑5小时后,施工速度因故减少到5米/时,结果两队同时完成任务,求乙队从开修到完工所修水渠的长度为多少米?
【答案】
(1)y=10x;y=20x﹣30
(2)
解:根据题意得:20x﹣30>10x,
20x﹣10x>30,
解得:x>3.
故开修3小时后,乙队修筑的水渠长度开始超过甲队
(3)
解:
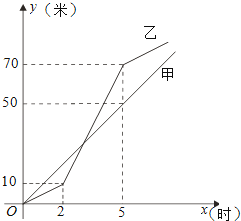
由图象得,甲队的速度是50÷5=10(米/时)
设:乙队从开修到完工所修水渠的长度为m米.
根据题意得: ![]() ,
,
解得:m=90.
答:乙队从开修到完工所修水渠的长度为90米.
【解析】解:(1)①设函数的解析式是y=kx,根据题意得:5k=50,解得:k=10,
则甲的函数解析式是:y=10x.
②设函数的解析式是:y=mx+b,
根据题意得: ![]() ,解得:
,解得: ![]() .
.
则函数解析式是:y=20x﹣30.

练习册系列答案
相关题目