题目内容
【题目】如图,已知函数 y=x+1 的图象与 y 轴交于点 A,一次函数 y=kx+b 的图象经过点 B(0,﹣1),与x 轴 以及 y=x+1 的图象分别交于点 C、D,且点 D 的坐标为(1,n),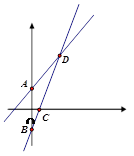
(1)则n= ,k= ,b= ;
(2)函数 y=kx+b 的函数值大于函数 y=x+1 的函数值,则X的取值范围是 ;
(3)求四边形 AOCD 的面积;
(4)在 x轴上是否存在点 P,使得以点 P,C,D 为顶点的三角形是直角三角形?若存在求出点 P 的坐标; 若不存在,请说明理由.
【答案】
(1)2,3,-1
(2)![]()
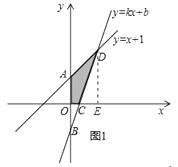
(3)解:过D作 ![]() 垂直于
垂直于 ![]() 轴,如图1所示,
轴,如图1所示,
则 ![]()
![]()
![]()
(4)解:如图2, 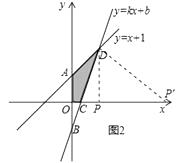
在 ![]() 轴上存在点P,使得以点P、C、D为顶点的三角形是直角三角形,
轴上存在点P,使得以点P、C、D为顶点的三角形是直角三角形,
理由:分两种情况考虑:
当 ![]() 时,可得
时,可得 ![]()
![]() 斜率为3,
斜率为3,
![]() 斜率为
斜率为 ![]() ,
, ![]()
![]() 解析式为
解析式为 ![]() 令
令 ![]() 即
即 ![]() 当
当 ![]() 时,由D横坐标为1,得到P点横坐标为1,
时,由D横坐标为1,得到P点横坐标为1, ![]() 在
在 ![]() 轴上,
轴上,
![]()
【解析】(1)用待定系数法求出n、k、b的值;(2)根据函数图像和D点的坐标求出X的取值范围;(3)根据图像得到S四边形AOCD=S梯形AOEDS△CDE
求出四边形 AOCD 的面积;(4)分两种情况讨论,当DP'⊥DC时,由直线DC的斜率为3,得到直线P'D斜率为![]() ,求出直线P'D解析式,由D横坐标为1,得到P点横坐标为1,得到P点的坐标.
,求出直线P'D解析式,由D横坐标为1,得到P点横坐标为1,得到P点的坐标.
【考点精析】利用确定一次函数的表达式对题目进行判断即可得到答案,需要熟知确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目