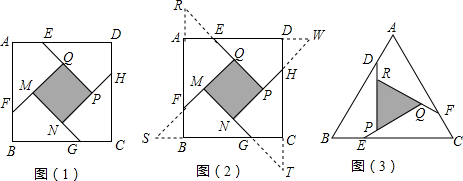
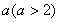题目内容
阅读下面材料:
小明遇到这样一个问题:
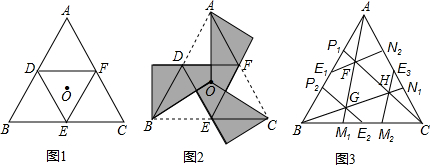
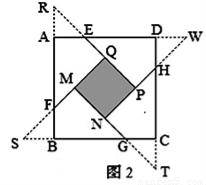
我们定义:如果一个图形绕着某定点旋转一定的角度α (0°<α<360°) 后所得的图形与原图形重合,则称此图形是旋转对称图形.如等边三角形就是一个旋转角为120°的旋转对称图形.如图1,点O是等边三角形△ABC的中心,D、E、F分别为AB、BC、CA的中点,请你将△ABC分割并拼补成一个与△ABC面积相等的新的旋转对称图形.

小明利用旋转解决了这个问题,图2中阴影部分所示的图形即是与△ABC面积相等的新的旋转对称图形.
请你参考小明同学解决问题的方法,利用图形变换解决下列问题:
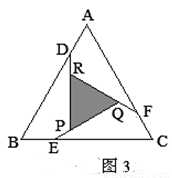
如图3,在等边△ABC中,E1、E2、E3分别为AB、BC、CA 的中点,P1、P2,M1、M2,N1、N2分别为AB、BC、CA的三等分点.
(1)在图3中画出一个和△ABC面积相等的新的旋转对称图形,并用阴影表示(保留画图痕迹);
(2)若△ABC的面积为a,则图3中△FGH的面积为______.
 解:(1)如图所示:
解:(1)如图所示:(答案不唯一);
(2)结合图中所有阴影部分可以分为7个全等的三角形每一个与△FGH的面积相等,故△FGH的面积为的
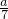 .
.故答案为:
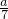 .
.分析:(1)根据旋转的性质旋转前后图形面积相等即可得出符合要求的答案;
(2)根据(1)中图形的性质,可以得出阴影部分可以分为7个全等的三角形每一个与△FGH的面积相等,进而得出答案即可.
点评:此题主要考查了利用旋转设计图案,几何旋转性质得出答案是解题关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目