题目内容
 如图,正方形ABCD的边长为4,点P在正方形内部,△BPC是等边三角形,连接PD、BD,那么△BPD的面积为
如图,正方形ABCD的边长为4,点P在正方形内部,△BPC是等边三角形,连接PD、BD,那么△BPD的面积为考点:正方形的性质,等边三角形的性质
专题:几何图形问题
分析:根据三角形面积计算公式,结合图形得到△BPD的面积=△BCP的面积+△CDP面积-△BCD的面积,列式进行计算求得答案即可.
解答:解:如图,
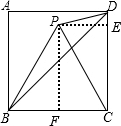
过P作PE⊥CD,PF⊥BC,
∵正方形ABCD的边长是4,△BPC为正三角形,
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCE=30°
∴PF=PB•sin60°=4×
=2
,PE=PC•sin30°=2,
S△BPD=S四边形PBCD-S△BCD=S△PBC+S△PDC-S△BCD=
×4×2
+
×2×4-
×4×4=4
+4-8=4
-4.
故答案为:4
-4.

过P作PE⊥CD,PF⊥BC,
∵正方形ABCD的边长是4,△BPC为正三角形,
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCE=30°
∴PF=PB•sin60°=4×
| ||
| 2 |
| 3 |
S△BPD=S四边形PBCD-S△BCD=S△PBC+S△PDC-S△BCD=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:4
| 3 |
点评:本题考查的正方形的性质以及等积变换,解答此题的关键是作出辅助线,利用锐角三角函数的定义求出PE及PF的长,再根据三角形的面积公式得出结论.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若多项式x2-2kxy-3y2+
xy-x-100中不含xy项,则k取( )
| 1 |
| 2 |
| A、1 | ||
| B、-1 | ||
C、
| ||
| D、0 |