题目内容
如下图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE。
(1)试探究,四边形BECF是什么特殊的四边形?
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论。
(特别提醒:表示角最好用数字)
(1)试探究,四边形BECF是什么特殊的四边形?
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论。
(特别提醒:表示角最好用数字)

解:(1)四边形BECF是菱形。
证明:BC的垂直平分线为EF,
∴BF=FC,BE=EC,
∴∠1=∠3,
∵∠ACB=90°,
∴∠1+∠2=90°,∠3+∠4=90°,
∴∠2=∠4,
∴EC=AE,
又∵CF=AE,BE=EC
∴BE=EC=CF=BF,
∴四边形BECF是菱形;
(2)当∠A=45°时,菱形BECF是正方形。
证明:∵∠A=45°,∠ACB=90°,
∴∠1=45°,
∴∠EBF=2∠A=90°,
∴菱形BECF是正方形。

证明:BC的垂直平分线为EF,
∴BF=FC,BE=EC,
∴∠1=∠3,
∵∠ACB=90°,
∴∠1+∠2=90°,∠3+∠4=90°,
∴∠2=∠4,
∴EC=AE,
又∵CF=AE,BE=EC
∴BE=EC=CF=BF,
∴四边形BECF是菱形;
(2)当∠A=45°时,菱形BECF是正方形。
证明:∵∠A=45°,∠ACB=90°,
∴∠1=45°,
∴∠EBF=2∠A=90°,
∴菱形BECF是正方形。


练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 24、如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
24、如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.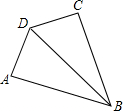 如图,已知:在四边形ABCD中,AD=DC=1,∠DCB=∠DAB=90°,BD=2,则四边形ABCD面积为
如图,已知:在四边形ABCD中,AD=DC=1,∠DCB=∠DAB=90°,BD=2,则四边形ABCD面积为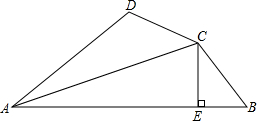 如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°,
如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°,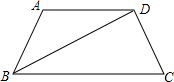 如图,已知,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,CD=4cm,∠ABC=∠DCB,求BC的长.
如图,已知,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,CD=4cm,∠ABC=∠DCB,求BC的长.