题目内容
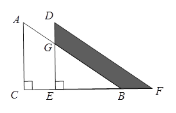
【题目】如图,已知直角梯形![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一动点,过
边上的一动点,过![]() 作线段
作线段![]() 的垂直平分线,交
的垂直平分线,交![]() 于点
于点![]() ,并交射线
,并交射线![]() 于点
于点![]() .
.
(1)如图1,当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的长;
的长;
(2)设![]() ,
,![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)如图2,联结![]() ,当
,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长.
的长.



【答案】(1)BC=5;(2)![]() ;(3)
;(3)![]() 的长为
的长为![]() 或3或
或3或![]() .
.
【解析】
(1)根据垂直平分线性质可知![]() ,设
,设![]() ,
,![]() ,在
,在![]() 中用勾股定理求出
中用勾股定理求出![]() ,即可解答;
,即可解答;
(2)联结![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,消去二次项即可得到
,消去二次项即可得到![]() 与
与![]() 的函数关系式;根据点
的函数关系式;根据点![]() 是
是![]() 边上的一动点结合(1)即可得出
边上的一动点结合(1)即可得出![]() 的定义域;
的定义域;
(3)分三种情况讨论,分别画出图形,根据相等的边用勾股定理列方程求解即可.
解:(1)∵梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
又∵![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)联结![]() ,
,![]() ,
,
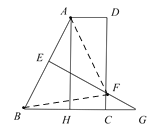
∵![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]()
∵![]() ,
,![]() ,
,
∴![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
∴![]()
∴![]()
(3)在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]()
当![]() 是等腰三角形时
是等腰三角形时
①∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
②![]()
取![]() 中点
中点![]() ,联结
,联结![]()
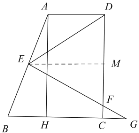
∵![]() 为
为![]() 的中点
的中点
∴![]() 为梯形中位线
为梯形中位线
∴![]()
∵![]()
∴![]() 为
为![]() 中点,
中点,
∴此时![]() 与
与![]() 重合
重合
∴![]()
③![]()
联结![]() 并延长交
并延长交![]() 延长线于点
延长线于点![]()
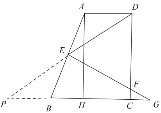
此时![]() .
.
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∴在![]() 中,
中,![]() ,
,
∵![]()
∴解得![]() ,
,![]() (不合题意含去)
(不合题意含去)
∴综上所述,当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长为
的长为![]() 或3或
或3或![]()

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目