题目内容
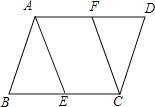
【题目】如图，一张纸片的形状为直角三角形，其中
，
，
，沿直线AD折叠该纸片，使直角边AC与斜边上的AE重合，则CD的长为______cm．
【答案】3
【解析】
在Rt△ABC中根据勾股定理得AB=20，再根据折叠的性质得AE=AC=6，DE=DC，∠AED=∠C=90°，所以BE=AB-AE=4，设CD=x，则BD=8-x，然后在Rt△BDE中利用勾股定理得到42+x2=（8-x）2，再解方程求出x即可．
在Rt△ABC中，
∵AC=6，BC=8，
∴AB=
=10，
∵△ACB沿直线AD折叠该纸片，使直角边AC与斜边上的AE重合，
∴AE=AC=6，DE=DC，∠AED=∠C=90°，
∴BE=AB-AE=10-6=4，
设CD=x，则BD=8-x，
在Rt△BDE中，
∵BE2+DE2=BD2，
∴42+x2=（8-x）2，解得x=3，
即CD的长为3cm．
故答案为：3
【题目】甲、乙两所学校共82人参加文艺汇演（其中甲校人数多于乙校人数，且甲校人数小于80人），如果两所学校分别购买服装，共付款6060元.
购买服装套数 | 1～40 | 41～80 | 81套及81套以上 |
每套服装价格 | 80元 | 70元 | 60元 |
（1）如果甲、乙两所学校联合起来购买服装，那么比各自购买服装一共可以节约多少钱？
（2）甲、乙两所学校各有多少学生参加演出？
（3）如果乙学校单独购买时，服装厂每件服装获利60%，丙学校购买的服装比乙多15套，那么服装厂卖给丙学校服装时共获利多少元？
【题目】某校招聘一名数学老师，对应聘者分别进行了教学能力、科研能力和组织能力三项测试，其中甲、乙两名应聘者的成绩如右表：（单位：分）
教学能力 | 科研能力 | 组织能力 | |
甲 | 81 | 85 | 86 |
乙 | 92 | 80 | 74 |
（1）若根据三项测试的平均成绩在甲、乙两人中录用一人，那么谁将被录用？
（2）根据实际需要，学校将教学、科研和组织能力三项测试得分按 5：3：2 的比确定每人的最后成绩，若按此成绩在甲、乙两人中录用一人，谁将被录用？
