Question

【题目】如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分，这点叫做这条折线的“折中点”．如果点D是折线A﹣C﹣B的“折中点”，请解答以下问题：

（1）已知AC=m，BC=n．

当m＞n时，点D在线段　 　上；

当m=n时，点D与　 　重合；

当m＜n时，点D在线段　 上；

（2）若E为线段AC中点，EC=4，CD=3，求CB的长度．

Answer 1

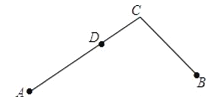
【答案】（1）AC，C，BC；（2）2或14．

【解析】试题分析：（1）根据题意和线段的和差关系即可得到结论；（2）分两种情况求解:①点D在线段AC上，由E为线段AC中点，EC=4，得到AC=2CE=8，于是得到AD=AC-CD=5，根据线段的和差即可得到结论；②点D在线段BC上，由E为线段AC中点，EC=4，得到AC=2CE=8，于是得到AD=AC-CD=5，根据线段的和差即可得到结论．

试题解析：

（1）已知AC=m，BC=n．

当m＞n时，点D在线段AC上；

当m=n时，点D与C重合；

当m＜n时，点D在线段BC上．

故答案为：AC，C，BC；

（2）点D在线段AC上

∵E为线段AC中点，EC=4，

AC=2CE=8，∵CD=3，

∴AD=AC﹣CD=5，

∵BD=AD=5，

∴BC=5﹣3=2；

点D在线段BC上，

∵E为线段AC中点，EC=4，

∴AC=2CE=8，∵CD=3，

∴AD=AC+CD=11，

∵BD=AD=11，

∴BC=11+3=14．

点睛:本题考查了线段中点的定义及线段的和差倍分的计算,根据图形找出线段之间的关系是解题的关键.