题目内容
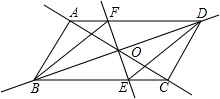
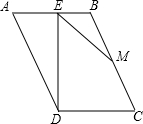 如图,平行四边形ABCD中,BC=2AB,DE⊥AB,M是BC的中点,∠BEM=50°,则∠B的大小是
如图,平行四边形ABCD中,BC=2AB,DE⊥AB,M是BC的中点,∠BEM=50°,则∠B的大小是
- A.100°
- B.110°
- C.120°
- D.135°
A
分析:可取AD的中点N,连接MN,MD,NE,如下图所示,可得MN平行AB、CD且垂直DE,进而得出∠5与∠4、∠3、∠2之间的关系,最终可求解∠B的大小.
解答: 解:如图,取AD的中点N,连接MN,MD,NE.
解:如图,取AD的中点N,连接MN,MD,NE.
∴AN=DN,
∵四边形ABCD是平行四边形,
∴AN∥BM,AB∥CD,
∴四边形ANMB是平行四边形,
∴AB∥MN,
∴MN∥CD,
∵BC=2AB,
∴MC=CD,∠1=∠2.
∴∠1=∠3
∴∠2=∠3.
又N是Rt△AED的斜边AD的中点,
∴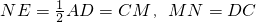 .
.
又N是Rt△AED的斜边AD的中点,∴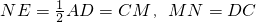 .
.
又MN是DE的中垂线,ME=MD
∵△EMN≌△MDC,
∴∠4=∠1=∠3.又∠4=∠5,
∴∠2=∠3=∠4=∠5=50°,
∴∠B=150°-50°=100°.
∴故选A.
点评:本题主要考查平行四边形及全等三角形的性质,熟练掌握其性质,能够求解一些简单的计算问题.
分析:可取AD的中点N,连接MN,MD,NE,如下图所示,可得MN平行AB、CD且垂直DE,进而得出∠5与∠4、∠3、∠2之间的关系,最终可求解∠B的大小.
解答:
 解:如图,取AD的中点N,连接MN,MD,NE.
解:如图,取AD的中点N,连接MN,MD,NE.∴AN=DN,
∵四边形ABCD是平行四边形,
∴AN∥BM,AB∥CD,
∴四边形ANMB是平行四边形,
∴AB∥MN,
∴MN∥CD,
∵BC=2AB,
∴MC=CD,∠1=∠2.
∴∠1=∠3
∴∠2=∠3.
又N是Rt△AED的斜边AD的中点,
∴
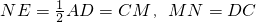 .
.又N是Rt△AED的斜边AD的中点,∴
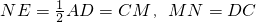 .
.又MN是DE的中垂线,ME=MD
∵△EMN≌△MDC,
∴∠4=∠1=∠3.又∠4=∠5,
∴∠2=∠3=∠4=∠5=50°,
∴∠B=150°-50°=100°.
∴故选A.
点评:本题主要考查平行四边形及全等三角形的性质,熟练掌握其性质,能够求解一些简单的计算问题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 次方程x2-7x+12=0的两个根,且OA>OB.
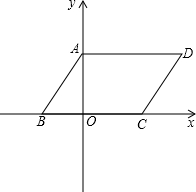
次方程x2-7x+12=0的两个根,且OA>OB.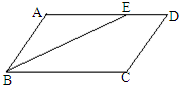 10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是
10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是
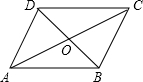 如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是
如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是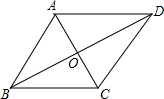 如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为
如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为