题目内容
如图(1),△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于点D,BE⊥MN于点E.
(1)请说明:△ADC≌△CEB.
(2)请你探索线段DE,AD,EB间的等量关系,并说明理由;
(3)当直线MN绕点C旋转到图(2)的位置时,其它条件不变,线段DE,AD,EB又有怎样的等量关系?(不必说理由).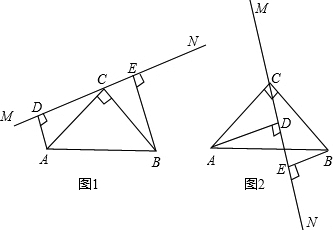
解:(1)理由:因为∠ACD+∠ACB+∠BCE=180°,∠ACB=90°,
所以∠ACD+∠BCE=90°.
又AD⊥MN,BE⊥MN,则∠ADC=∠CEB=90°,∠DAC+∠ACD=90°.
故∠DAC=∠ECB
而AC=CB.所以△ADC≌△CEB(AAS).
(2)等量关系:DE=AD+EB.
理由:由(1)知△ADC≌△CEB.则AD=CE,DC=EB.
因为DE=CE+DC,所以DE=AD+EB.
(3)等量关系:DE=AD-EB.
分析:(1)由全等直角三角形的判定定理AAS来证明△ADC≌△CEB;
(2)利用(1)的△ADC≌△CEB的对应边相等求得AD=CE,DC=EB;而DE=CE+DC,所以DE=AD+EB;
(3)利用(2)的解答思路可以直接回答DE=AD-EB.
点评:本题考查了等腰直角三角形、全等三角形的判定与性质.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等(直角三角形除外),判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
所以∠ACD+∠BCE=90°.
又AD⊥MN,BE⊥MN,则∠ADC=∠CEB=90°,∠DAC+∠ACD=90°.
故∠DAC=∠ECB
而AC=CB.所以△ADC≌△CEB(AAS).
(2)等量关系:DE=AD+EB.
理由:由(1)知△ADC≌△CEB.则AD=CE,DC=EB.
因为DE=CE+DC,所以DE=AD+EB.
(3)等量关系:DE=AD-EB.
分析:(1)由全等直角三角形的判定定理AAS来证明△ADC≌△CEB;
(2)利用(1)的△ADC≌△CEB的对应边相等求得AD=CE,DC=EB;而DE=CE+DC,所以DE=AD+EB;
(3)利用(2)的解答思路可以直接回答DE=AD-EB.
点评:本题考查了等腰直角三角形、全等三角形的判定与性质.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等(直角三角形除外),判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
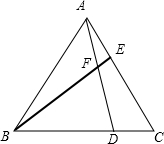 已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD.
已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD.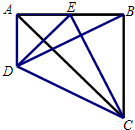 如图,在等腰直角△ABC中,∠ABC=90°,AB=BC,AD∥BC,E是AB的中点,BE=AD.
如图,在等腰直角△ABC中,∠ABC=90°,AB=BC,AD∥BC,E是AB的中点,BE=AD.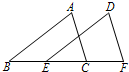 13、如图,△DEF是由△ABC平移得到的,若BC=6cm,E是BC的中点,则平移的距离是
13、如图,△DEF是由△ABC平移得到的,若BC=6cm,E是BC的中点,则平移的距离是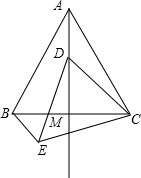 方作等边△CDE,连接BE.
方作等边△CDE,连接BE.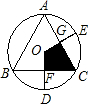 如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的
如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的