题目内容
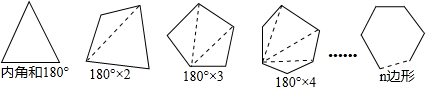
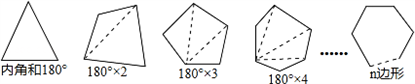
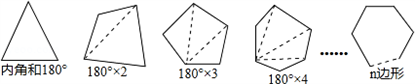
已知任意三角形的内角和为180°，试利用多边形中过某一点的对角线条数，寻求多边形内角和的公式．
根据上图所示，一个四边形可以分成________个三角形；于是四边形的内角和为________度：一个五边形可以分成________个三角形，于是五边形的内角和为________度，…，按此规律，n边形可以分成________个三角形，于是n边形的内角和为________度．
2 360 3 540 （n-2） （n-2）•180
分析：解决题目的方法是把多边形的问题转化为三角形的问题，把多边形的内角和，转化为三角形的角的和．
解答：根据图形所示，一个四边形可以分成2个三角形；于是四边形的内角和为 360度：一个五边形可以分成 3个三角形，于是五边形的内角和为 540度，…，按此规律，n边形可以分成 （n-2）个三角形，于是n边形的内角和为 （n-2）•180度．
故答案为：2；360：3，540，（n-2），（n-2）•180．
点评：本题通过多边形的对角线考查了多边形的内角和，解题关键是得出过多边形中某一顶点的对角线将多边形分成（n-2）个三角形．
分析：解决题目的方法是把多边形的问题转化为三角形的问题，把多边形的内角和，转化为三角形的角的和．
解答：根据图形所示，一个四边形可以分成2个三角形；于是四边形的内角和为 360度：一个五边形可以分成 3个三角形，于是五边形的内角和为 540度，…，按此规律，n边形可以分成 （n-2）个三角形，于是n边形的内角和为 （n-2）•180度．
故答案为：2；360：3，540，（n-2），（n-2）•180．
点评：本题通过多边形的对角线考查了多边形的内角和，解题关键是得出过多边形中某一顶点的对角线将多边形分成（n-2）个三角形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
