题目内容
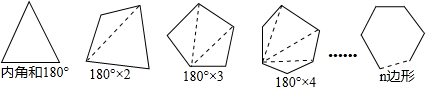
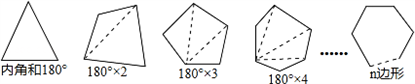
已知任意三角形的内角和为180°,试利用多边形中过某一点的对角线条数,寻求多边形内角和的公式.根据下图所示,
一个四边形可以分成 _________ 个三角形;于是四边形的内角和为 _________ 度:
一个五边形可以分成 _________ 个三角形,于是五边形的内角和为 _________ 度,…,
按此规律,n边形可以分成 _________ 个三角形,于是n边形的内角和为 _________ 度.
一个四边形可以分成 _________ 个三角形;于是四边形的内角和为 _________ 度:
一个五边形可以分成 _________ 个三角形,于是五边形的内角和为 _________ 度,…,
按此规律,n边形可以分成 _________ 个三角形,于是n边形的内角和为 _________ 度.
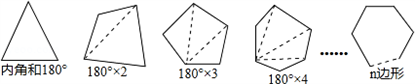
解:根据图形所示,一个四边形可以分成2个三角形;于是四边形的内角和为 360度:
一个五边形可以分成 3个三角形,于是五边形的内角和为 540度,…,
按此规律,n边形可以分成 (n﹣2)个三角形,于是n边形的内角和为 (n﹣2)180度.
故答案为:2;360:3,540,(n﹣2),(n﹣2)180.
一个五边形可以分成 3个三角形,于是五边形的内角和为 540度,…,
按此规律,n边形可以分成 (n﹣2)个三角形,于是n边形的内角和为 (n﹣2)180度.
故答案为:2;360:3,540,(n﹣2),(n﹣2)180.

练习册系列答案
相关题目