题目内容
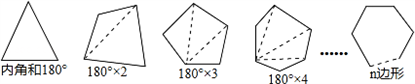
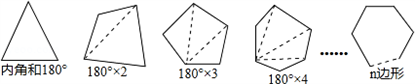
已知任意三角形的内角和为180°,利用三角形探求多边形内角和的公式.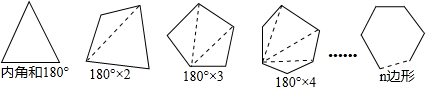
(1)过四边形一个顶点的对角线将它分成两个三角形,于是四边形的内角和为 度;类似地可得五边形的内角和为 度;…,按此规律,过n边形一个顶点的对角线将n边形可以分成 个三角形,于是n边形的内角和为 度.
(2)根据以上得出的规律,求正八边形的每个内角的度数.

(1)过四边形一个顶点的对角线将它分成两个三角形,于是四边形的内角和为
(2)根据以上得出的规律,求正八边形的每个内角的度数.
分析:(1)根据图形计算出四边形、五边形的内角和,再根据计算,过n边形一个顶点的对角线将n边形可以分成的三角形的个数比边数少2,然后利用三角形的内角和定理计算即可得到n边形的内角和;
(2)用正八边形内角和除以8计算即可得解.
(2)用正八边形内角和除以8计算即可得解.
解答:解:(1)过四边形一个顶点的对角线将它分成两个三角形,于是四边形的内角和为360度;
类似地可得五边形的内角和为540度;
…,
按此规律,过n边形一个顶点的对角线将n边形可以分成(n-2)个三角形,于是n边形的内角和为(n-2)•180度;
故答案为:360,540,(n-2),(n-2)•180.
(2)
=135°.
类似地可得五边形的内角和为540度;
…,
按此规律,过n边形一个顶点的对角线将n边形可以分成(n-2)个三角形,于是n边形的内角和为(n-2)•180度;
故答案为:360,540,(n-2),(n-2)•180.
(2)
| (8-2)•180° |
| 8 |
点评:本题是对图形变化规律的考查,比较简单,观察出过n边形一个顶点的对角线将n边形可以分成的三角形的个数比边数少2是解题的关键.

练习册系列答案
相关题目