题目内容
【题目】如图,∠AOB=30°,OC平分∠AOB,P为OC上任意一点,PD∥OA交OB于D,PE⊥OA于E,若OD=4,则PE= __________.
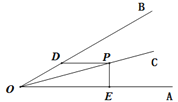
【答案】2
【解析】
过P作PF⊥OB于F,根据角平分线的定义可得∠AOC=∠BOC=15°,根据平行线的性质可得∠DPO=∠AOP=15°,从而可得PD=OD,再根据30度所对的边是斜边的一半可求得PF的长,最后根据角平分线的性质即可求得PE的长.
解:过P作PF⊥OB于F,
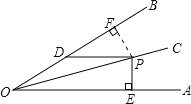
∵∠AOB=30°,OC平分∠AOB,
∴∠AOC=∠BOC=15°,
∵PD∥OA,
∴∠DPO=∠AOP=15°,
∴∠BOC=∠DPO,
∴PD=OD=4,
∵∠AOB=30°,PD∥OA,
∴∠BDP=30°,
∴在Rt△PDF中,PF=![]() PD=2,
PD=2,
∵OC为角平分线,PE⊥OA,PF⊥OB,
∴PE=PF,
∴PE=PF=2.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目