题目内容
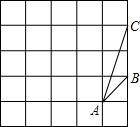
如图，四边形ABGH，四边形BCFG，四边形CDEF都是正方形，图中与△HBC相似的三角形为（ ）
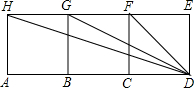
| A．△HBD | B．△HCD | C．△HAC | D．△HAD |
设正方形ABGH的边长为1，运用勾股定理得HB=
，HC=
，则HC：HB：BC=
：
：1．
A、∵HB=
，BD=2，HD=
，∴HD：BD：HB=
：2：
=
：
：1，∴HC：HB：BC=HD：BD：HB，∴△HBC∽△DBH，故本选项正确；
B、∵HC=
，CD=1，HD=
，∴HD：HC：CD=
：
：1，∴HC：HB：BC≠HD：HC：CD，∴△HBC与△HCD不相似，故本选项错误；
C、∵HA=1，AC=2，HC=
，HC：AC：HA=
：2：1，∴HC：HB：BC≠HC：AC：HA，∴△HBC与△HAC不相似，故本选项错误；
D、∵HA=1，AD=3，HD=
，HD：AD：HA=
：3：1，∴HC：HB：BC≠HD：AD：HA，∴△HBC与△HAD不相似，故本选项错误．
故选A．
| 2 |
| 5 |
| 5 |
| 2 |
A、∵HB=
| 2 |
| 10 |
| 10 |
| 2 |
| 5 |
| 2 |
B、∵HC=
| 5 |
| 10 |
| 10 |
| 5 |
C、∵HA=1，AC=2，HC=
| 5 |
| 5 |
D、∵HA=1，AD=3，HD=
| 10 |
| 10 |
故选A．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
