Question

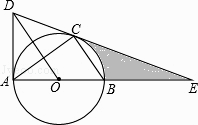
【题目】如图，四边形ABCD中，AB=AD，CB=CD，AB ∥ CD.

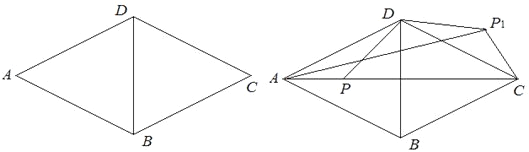
（1）求证：四边形ABCD是菱形.

（2）当△ABD满足什么条件时，四边形ABCD是正方形.（直接写出一个符合要求的条件）.

（3）对角线AC和BD交于点O，∠ ADC =120°，AC=8， P为对角线AC上的一个动点，连接DP，将DP绕点D逆时针方向旋转120°得到线段DP1，直接写出A P1的取值范围.

Answer 1

【答案】(1)见解析;(2)见解析;(3) .

【解析】（1）先证明四边形ABCD是平行四边形，然后证明它是菱形即可.

（2）由（1）已知四边形ABCD是菱形，所以当△ABD是直角三角形时，四边形ABCD是正方形.

（3）将线段AC顺时针方向旋转60°得到线段CE，并连接AE，点到直线的距离垂线段最短，所以AP1垂直CE时，AP1取最小值，点P1在E点，AP1取最大值，即可求解.

证明：（1） AB=AD，CB=CD，∴∠ABD=∠ADB，∠CBD=∠CDB，

∵AB∥CD，∴∠ABD=∠CDB，∴∠ADB=∠CBD，

∴AD∥BC，∴四边形ABCD是平行四边形.

又∵AB=AD，∴四边形ABCD是菱形.

（2）要使四边形ABCD是正方形，则∠A=∠ABC=∠C=∠ADC=90°，

∴当△ABD是直角三角形时，即∠BAD=90°时，四边形ABCD是正方形；

（3）以点C为中心，将线段AC顺时针方向旋转60°得到线段CE，由题意可知，点P1在线段CE上运动.

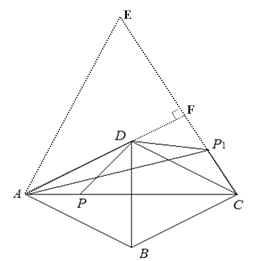
连接AE，

∵AC=CE，∠ACE=60°，∴△ACE为等边三角形，

∴AC=CE=AE=8，过点A作于点F，

∴.当点P1在点F时，线段AP1最短，此时；.

当点P1在点E时，线段AP1最长，此时AP1=8，

..