题目内容
 如图,△ABC是等边三角形,D是BC延长线上任意一点,以AD为一边向右侧作等边△ADE,连接CE.
如图,△ABC是等边三角形,D是BC延长线上任意一点,以AD为一边向右侧作等边△ADE,连接CE.
(1)求证:△CAE≌△BAD;
(2)判断直线AB与EC的位置关系,并说明理由.
(1)∵△ADE与△ABC都是等边三角形,
∴AC=AB,AE=AD,∠DAE=∠BAC=60°
∴∠DAE+∠CAD=∠BAC+∠CAD
即∠CAE=∠BAD
∴在△CAE与△BAD中,
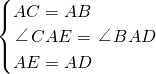
∴△CAE≌△BAD、
(2)EC∥AB、
由△CAE≌△BAD,
∴∠ACE=∠B=60°,
∴∠ACE=∠BAC=60°,
∴EC∥AB
分析:(1)根据△ADE与△ABC都是等边三角形,得到AC=AB,AE=AD,∠DAE=∠BAC=60°,从而得到∠DAE+∠CAD=∠BAC+∠CAD、即∠CAE=∠BAD,利用SAS证得△CAE≌△BAD;
(2)由△CAE≌△BAD,得到∠ACE=∠B=60°,∠ACE=∠BAC=60°,利用内错角相等证得EC∥AB.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质,根据等边三角形中隐含的条件可以得到证明三角形全等的一些条件.
∴AC=AB,AE=AD,∠DAE=∠BAC=60°
∴∠DAE+∠CAD=∠BAC+∠CAD
即∠CAE=∠BAD
∴在△CAE与△BAD中,
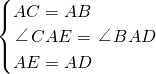
∴△CAE≌△BAD、
(2)EC∥AB、
由△CAE≌△BAD,
∴∠ACE=∠B=60°,
∴∠ACE=∠BAC=60°,
∴EC∥AB
分析:(1)根据△ADE与△ABC都是等边三角形,得到AC=AB,AE=AD,∠DAE=∠BAC=60°,从而得到∠DAE+∠CAD=∠BAC+∠CAD、即∠CAE=∠BAD,利用SAS证得△CAE≌△BAD;
(2)由△CAE≌△BAD,得到∠ACE=∠B=60°,∠ACE=∠BAC=60°,利用内错角相等证得EC∥AB.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质,根据等边三角形中隐含的条件可以得到证明三角形全等的一些条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
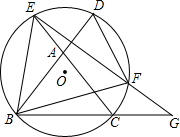 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G. 9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角
9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角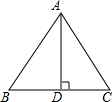 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于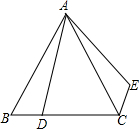 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是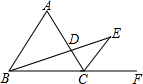 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.