题目内容
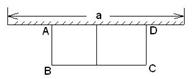
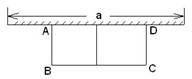
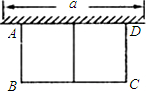 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花辅,设花圃的宽AB为x(m),面积为y(m2),求:
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花辅,设花圃的宽AB为x(m),面积为y(m2),求:(1)求y与x的函数关系式
(2)如果要围成面积为45m2的花圃,AB的长度是
分析:(1)已知AB=X,BC=24-3x,则y=-3x2+24x.易求x的取值范围.
(2)当y=45时,根据实际情况求出x的值即可.
(2)当y=45时,根据实际情况求出x的值即可.
解答:解: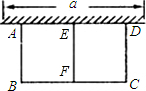
(1)∵宽AB=xm,
∵BC+CD+EF+AB=24,CD=EF=AB=xm,
∴长BC=24-3x,
∴y=-3x2+24x,
又x>0,且10≥24-3x>0,
∴
≤x<8.
(2)当y=45时,即-3x2+24x=45,
∴x=3(舍去)或x=5.
∴当AB为5m时,面积为45m2.

(1)∵宽AB=xm,
∵BC+CD+EF+AB=24,CD=EF=AB=xm,
∴长BC=24-3x,
∴y=-3x2+24x,
又x>0,且10≥24-3x>0,
∴
| 14 |
| 3 |
(2)当y=45时,即-3x2+24x=45,
∴x=3(舍去)或x=5.
∴当AB为5m时,面积为45m2.
点评:本题考查的是二次函数的应用,难度简单.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 20、如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm.
20、如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm.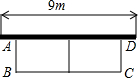 长方形养鸡场.设养鸡场的长BC为xm,面积为ym2.
长方形养鸡场.设养鸡场的长BC为xm,面积为ym2.