题目内容
【题目】如图,已知AE⊥FE,垂足为E,且E是DC的中点.
(1)如图①,如果FC⊥DC,AD⊥DC,垂足分别为C,D,且AD=DC,判断AE是∠FAD的角平分线吗?(不必说明理由)
(2)如图②,如果(1)中的条件“AD=DC”去掉,其余条件不变,(1)中的结论仍成立吗?请说明理由;
(3)如图③,如果(1)中的条件改为“AD∥FC”,(1)中的结论仍成立吗?请说明理由.

【答案】(1)AE是∠FAD的角平分线(2)成立(3)成立
【解析】
见详解
(1)AE是∠FAD的角平分线;
(2)成立,如图,延长FE交AD于点B,
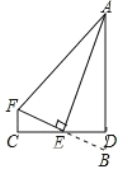
∵E是DC的中点,
∴EC=ED,
∵FC⊥DC,AD⊥DC,
∴∠FCE=∠EDB=90°,
在△FCE和△BDE中,
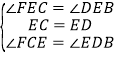 ,
,
∴△FCE≌△BDE,
∴EF=EB,
∵AE⊥FE,
∴AF=AB,
∴AE是∠FAD的角平分线;
(3)成立,如图,延长FE交AD于点B,
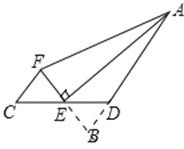
∵AD=DC,
∴∠FCE=∠EDB,
在△FCE和△BDE中,
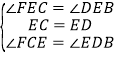 ,
,
∴△FCE≌△BDE,
∴EF=EB,
∵AE⊥FE,
∴AF=AB,
∴AE是∠FAD的角平分线.

练习册系列答案
相关题目






