题目内容
同一个圆的内接正六边形和外切正六边形的周长的比等于
- A.3:4
- B.
 :2
:2 - C.2:

- D.1:2
B
分析:先根据题意画出图形,设圆的半径为1,分别求出其内接正六边形和外切正六边形的边长即可求解.
解答: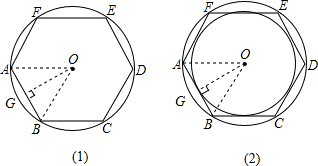 解:设圆的半径为1,
解:设圆的半径为1,
如图(1),
连接OA、OB过O作OG⊥AB;
∵六边形ABCDEF为正六边形,
∴∠AOB= =60°;
=60°;
∵OA=OB,OG⊥AB,
∴∠AOG= =30°,
=30°,
∴AG=OA•sin30°=1× =
= ,
,
∴AB=2AG=2× =1,
=1,
∴C六边形ABCD=6AB=6.
如图(2)连接OA、OB过O作OG⊥AB;
∵六边形ABCDEF为正六边形,
∴∠AOB= =60°,
=60°,
∵OA=OB,OG⊥AB,
∴∠AOF= =30°,
=30°,
∴AG=OG•tan30°= ,
,
∴AB=2AG=2× =
= ,
,
∴C六边形ABCDEF=6AB=6× =4
=4 cm.
cm.
∴圆的内接正六边形和外切正六边形的周长的比=6:4 =
= :2.
:2.
点评:本题考查学生对正多边形的概念掌握和计算的能力.
解答这类题往往一些学生因对正多边形的基本知识不明确,将多边形的半径与内切圆的半径相混淆而造成错误计算.
分析:先根据题意画出图形,设圆的半径为1,分别求出其内接正六边形和外切正六边形的边长即可求解.
解答:
 解:设圆的半径为1,
解:设圆的半径为1,如图(1),
连接OA、OB过O作OG⊥AB;
∵六边形ABCDEF为正六边形,
∴∠AOB=
 =60°;
=60°;∵OA=OB,OG⊥AB,
∴∠AOG=
 =30°,
=30°,∴AG=OA•sin30°=1×
 =
= ,
,∴AB=2AG=2×
 =1,
=1,∴C六边形ABCD=6AB=6.
如图(2)连接OA、OB过O作OG⊥AB;
∵六边形ABCDEF为正六边形,
∴∠AOB=
 =60°,
=60°,∵OA=OB,OG⊥AB,
∴∠AOF=
 =30°,
=30°,∴AG=OG•tan30°=
 ,
,∴AB=2AG=2×
 =
= ,
,∴C六边形ABCDEF=6AB=6×
 =4
=4 cm.
cm.∴圆的内接正六边形和外切正六边形的周长的比=6:4
 =
= :2.
:2.点评:本题考查学生对正多边形的概念掌握和计算的能力.
解答这类题往往一些学生因对正多边形的基本知识不明确,将多边形的半径与内切圆的半径相混淆而造成错误计算.

练习册系列答案
相关题目
同一个圆的内接正六边形和外切正六边形的周长的比等于( )
| A、3:4 | ||
B、
| ||
C、2:
| ||
| D、1:2 |
 :2
:2
 :2
:2
 :2
:2