题目内容
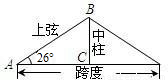
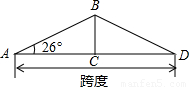如图，厂房屋顶人字架（等腰三角形）的跨度为10米，∠A=26°，则中柱BC（C为底边中点）的长约是 米（精确到0.01）附：①sin26°=0.4384
②cos26°=0.8988
③tan26°=0.4877
④cot26°=2.0503．
【答案】分析：先根据等腰三角形的性质求出AC的长，再根据BC=AC•tan∠A即可得出结论．
解答：解：∵△ABD是等腰三角形，C为底边中点，AD=10米，
∴BC⊥AD，AC=
AD=
×10=5米，
∴BC=AC•tan∠A=AC•tan26°=5×0.4877≈2.44（米）．
故答案为：2.44．
点评：本题考查的是解直角三角形的应用，熟知等腰三角形的性质及锐角三角函数的定义是解答此题的关键．
解答：解：∵△ABD是等腰三角形，C为底边中点，AD=10米，
∴BC⊥AD，AC=
AD=×10=5米，∴BC=AC•tan∠A=AC•tan26°=5×0.4877≈2.44（米）．
故答案为：2.44．
点评：本题考查的是解直角三角形的应用，熟知等腰三角形的性质及锐角三角函数的定义是解答此题的关键．
练习册系列答案
相关题目
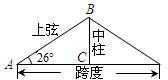如图，厂房屋顶人字架（等腰三角形）的跨度为12m，∠A=26°，则中柱BC（C为底边中点）的长约为
（1997•武汉）如图，厂房屋顶人字架（等腰三角形）的跨度为10米，∠A=26°，则中柱BC（C为底边中点）的长约是
，则中柱BC（C为底边中点）的长约为 m．（精确到0．01m）
