题目内容
已知抛物线y=ax2+bx+c（a≠0）经过点（-1，0），且顶点在第一象限．有下列三个结论：①a＜0；②a+b+c＞0；③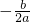
＞0．其中正确的结论有
- A.只有①
- B.①②
- C.①③
- D.①②③
D
分析：根据函数的图象的顶点的位置和经过的点的坐标确定其图象的大体位置，然后作出判断即可．
解答：∵抛物线y=ax2+bx+c（a≠0）经过点（-1，0），且顶点在第一象限，
∴其图象开口向下，
∴a＜0，
故①正确；
∵当x=1时，y＞0，
∴a+b+c＞0，
故②正确；
∵其对称轴在y轴右侧，
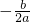∴＞0，
∴③也正确．
故选D．
点评：本题考查了二次函数的图象与系数的关系，解题时根据题目提供的条件画出函数图象的草图，然后根据草图叙述更为方便．
分析：根据函数的图象的顶点的位置和经过的点的坐标确定其图象的大体位置，然后作出判断即可．
解答：∵抛物线y=ax2+bx+c（a≠0）经过点（-1，0），且顶点在第一象限，
∴其图象开口向下，
∴a＜0，
故①正确；
∵当x=1时，y＞0，
∴a+b+c＞0，
故②正确；
∵其对称轴在y轴右侧，
∴
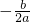＞0，∴③也正确．
故选D．
点评：本题考查了二次函数的图象与系数的关系，解题时根据题目提供的条件画出函数图象的草图，然后根据草图叙述更为方便．
练习册系列答案
阅读快车系列答案
相关题目
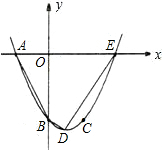与x轴的另一个交点为E．
如图，已知抛物线y=ax2+bx+c（其中b＞0，c＜0）的顶点P在x轴上，与y轴交于点Q，过坐标原点O，作OA⊥PQ，垂足为A，且OA=