题目内容
已知函数y=（m-4）xm2-5m+5+m-2，当m为何值时，它是一次函数，画出它的图象，并指出图象经过哪几个象限？y随x的增大而增大还是增大而减小？分析：根据一次函数的定义，令m2-5m+5=1且m-4≠0即可求出m的值，将m的值代入函数y=（m-4）xm2-5m+5+m-2，根据k、b的取值即可判断图象经过的象限及函数增减性．
解答：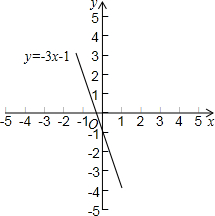
解：根据一次函数的定义，得：m2-5m+5=1，
解得m=4或m=1，
又∵m-4≠0，即m≠4，
∴当m=1时，这个函数是一次函数；
将m=1代入函数y=（m-4）xm2-5m+5+m-2，
可得：y=-3x-1，
作图如下：
∵k＜0，b＜0，
∴图象经过二、三、四象限，y随x的增大而减小．
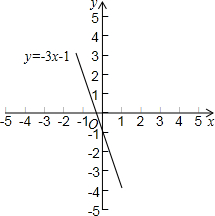解：根据一次函数的定义，得：m2-5m+5=1，解得m=4或m=1，
又∵m-4≠0，即m≠4，
∴当m=1时，这个函数是一次函数；
将m=1代入函数y=（m-4）xm2-5m+5+m-2，
可得：y=-3x-1，
作图如下：
∵k＜0，b＜0，
∴图象经过二、三、四象限，y随x的增大而减小．
点评：本题考查了一次函数的定义，及一次函数y=kx+b的图象性质及函数增减性．
练习册系列答案
相关题目